Go语言二叉树数据结构的应用
树的定义和基本术语
树是 n(n>=0) 个节点的有限集合 T。在任意一棵非空树中满足如下两个条件:- 有且仅有一个根节点(Root)。
- 当 n>1 时,其余节点可分为 m(m>=0) 个互不相交的有限集合 T1,T2,……,Tm,其中每一个集合本身又都是一棵树,并且称为根的子树(Subtree),如下图所示。
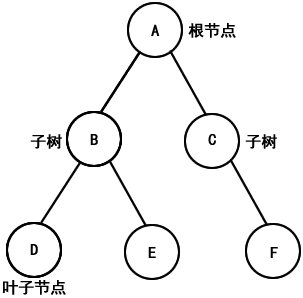
图:树型结构
由上图可知,树的定义是递归的,树是一种递归数据结构。树的这种定义为树的递归处理带来了很大方便,本节举例中几乎所有对树的处理都采用了递归算法。
在了解树型结构时,还有几个基本概念非常重要,必须要掌握:
- 节点的度:树中每个节点具有的子树数,或后继节点数称为该节点的度。
- 树的度:树中所有节点的度的最大值称为树的度。
- 分支节点:度大于 0 的节点称为分支节点或非终端节点。
- 叶子节点:度为 0 的节点称为叶子节点或终端节点。
- 儿子节点:一个节点的后继称为该节点的儿子节点。
- 父亲节点:一个节点称为其后继节点的父亲节点。
- 子孙节点:一个节点的所有子树中的节点称为该节点的子孙节点。
- 祖先节点:从根节点到达一个节点的路径上,通过的所有节点称为该节点的祖先节点。
- 兄弟节点:具有同一父亲的节点相互称为兄弟节点。
- 节点的层数:树是一种层次结构,根节点为第一层,其儿子节点为第二层,以此类推可以得到每个节点的层数。
- 树的深度:树中节点的最大层数称为树的深度或高度。
- 森林:0 个或多个不相交的树的集合称为森林。
二叉树简介
二叉树是一种特殊的树,具有如下特点:- 二叉树中每个节点最多有两棵子树,称为左子树、右子树;
- 左子树和右子树是有顺序的,有左右之分,次序不能随意颠倒;
- 即使某个节点只有一个子树,也要区分左右子树。
除了这些基本特征外,还有如下一些特殊的二叉树。
1) 斜树
所有的节点只有左子树则称为左斜树;所有节点只有右子树则称为右斜树。如下图所示: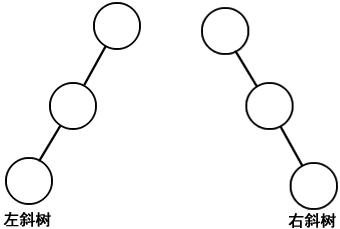
图:左斜树和右斜树
2) 满二叉树
在一棵二叉树中,所有的分支结点都存在左子树和右子树,并且所有的叶子结点都在同一层上,这样的二叉树称为满二叉树。就是完美圆满的意思。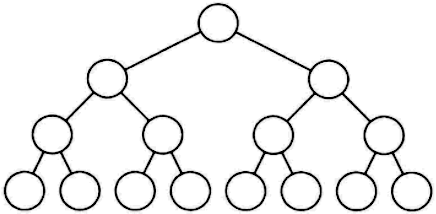
图:满二叉树
满二叉树的特点如下所示:
- 叶子只能出现在最下一层。
- 非叶子结点度一定是 2.
- 在同样深度的二叉树中,满二叉树的结点个数最多,叶子树最多。
3) 完全二叉树
在一棵二叉树中,除最后一层外,若其余各层都是满的,最后一层要么是满的,要么在右边缺少若干个连续的节点,这样的二叉树被称为完全二叉树。满二叉树必须是完全二叉树,而完全二叉树不一定是满二叉树。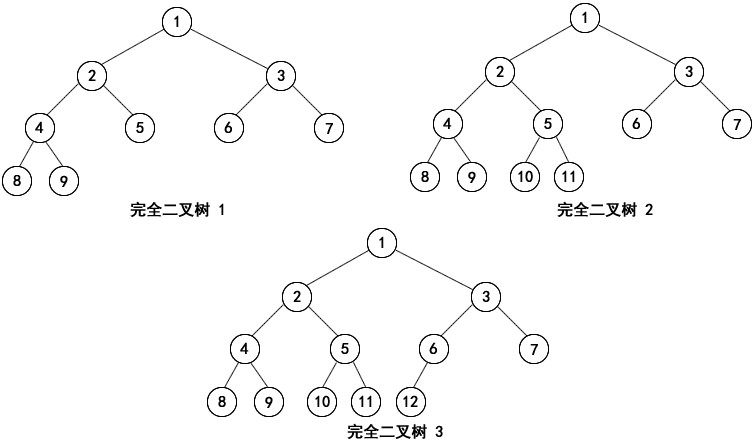
图:完全二叉树
完全二叉树的特点如下所示:
- 叶子结点只能出现在最下一层(满二叉树继承而来)。
- 最下层叶子结点一定集中在左部连续位置。
- 倒数第二层,如有叶子节点,一定出现在右部连续位置。
- 同样结点树的二叉树,完全二叉树的深度最小。
二叉树的链接存储结构
二叉树的存储方法有顺序存储、链接存储和线索树存储等几种存储方法,顺序存储是使用数组来完成,而链接存储和线索树存储都使用了链表来完成。本节在二叉树的应用举例中使用了链接存储法。节点定义
在二叉树的链接存储结构中,通常采用的方法是:每个节点设置三个域,即值域、左指针域和右指针域,其结构如下图所示。
图:二叉树链接存储结构
其中 Data 表示值域,用于存储放入节点中的数据元素,LeftChild 和 RightChild 分别表示左指针域和右指针域,用以分别存储左子树和右子树节点的指针地址。
链接存储的指针类型和节点定义如下:
type Node struct {
Left *Node
Data interface{}
Right *Node
}
接口定义
二叉树的应用处理功能主要包括:- 二叉树新节点的创建、初始化;
- 二叉树的输出、度的计算、叶子节点统计等基本操作;
- 二叉树的前序、中序、后序遍历等。
针对这些功能本例共定义了三个接口:Initer、Operater 和 Order。
1) Initer 接口
当为二叉树创建了一个新节点时,Initer 接口提供了 SetData() 方法可以对节点的 Data 字段进行初始化。Initer 接口定义如下:
type Initer interface {
SetData (data interface{})
}
2) Operater 接口
当已经生成了一个二叉树时,可以使用 Operater 接口提供的三个方法:PrintBT()、Depth() 和 LeafCount(),对二叉树进行输出、深度计算和叶子统计等基本操作。Operater 接口定义如下:
type Operater interface {
PrintBT()
Depth() int
LeafCount() int
}
3) Order 接口
对二叉树的遍历是一个重要的功能,这些功能在接口 Order 中实现,Order 接口中共定义了三个方法,分别是 PreOrder()、InOrder() 和 PostOrder(),分别可以实现前序遍历、中序遍历和后序遍历。Order 接口的定义如下:
type Order interface {
PreOrder()
InOrder()
PostOrder()
}
接口的意义也在于此,即同一个接口可以有不同的实现方式,甚至由不同的人去完成。
方法的实现
通过接口的概念知道接口是方法的组合,而在定义接口时不必马上实现方法,方法可由设计者自己或交由其他人单独设计。本例三个接口中共有 7 个方法,下面分别介绍一下它们是怎么实现的。1) SetData 方法
SetData() 通过空接口 interface{},可以将任意类型数据赋值给二叉树节点的 Data 字段,实现二叉树对任意数据类型的存储。SetData 方法的定义如下:
func (n *Node) SetData(data interface{}) {
n.Data = data
}
2) PrintBT 方法
PrintBT() 调用底层函数 PrintBT(),输出一个给定二叉树的嵌套括号表示。PrintBT 方法的定义如下:
func (n *Node) PrintBT() {
PrintBT(n)
}
3) Depth 方法
Depth() 调用底层函数 Depth(),返回二叉树的深度。Depth 方法的定义如下:
func (n *Node) Depth() int {
return Depth(n)
}
4) LeafCount 方法
LeafCount() 调用底层函数 LeafCount(),返回二叉树的叶子节点数。LeafCount 方法的定义如下:
func (n *Node) LeafCount() int {
return LeafCount(n)
}
5) PreOrder 方法
PreOrder() 调用底层函数 PreOrder() 对二叉树进行前序遍历。PreOrder 方法的定义如下:
func (n *Node) PreOrder() {
PreOrder(n)
}
6) InOrder 方法
InOrder() 调用底层函数 InOrder() 对二叉树进行中序遍历。InOrder 方法的定义如下:
func (n *Node) InOrder() {
InOrder(n)
}
7) PostOrder 方法
PostOrder() 调用底层函数 PostOrder() 对二叉树进行后序遍历。PostOrder 方法的定义如下:
func (n *Node) PostOrder() {
PostOrder(n)
}
底层函数设计
在面向对象程序设计中,上层方法的功能实现还要依赖底层函数,本例中大部分方法也是这样,现将所有底层函数一一列举如下。1) NewNode 函数
NewNode() 按照链接存储方式生成一个新的二叉树节点,参数 left 指向左指针域,参数 right 指向右指针域。NewNode 函数的定义如下:
func NewNode(left, right *Node) *Node {
return &Node{left, nil, right}
}
2) PrintBT 函数
PrintBT() 用于输出一个给定二叉树的嵌套括号表示,采用递归算法:- 首先输出根节点,然后再依次输出左子树和右子树,在输出左子树前打印输出左括号“(”,在输出右子树后打印输出右括号“)”;
- 另外,依次输出的左、右子树要至少有一个不为空,若都为空就不必输出了。
PrintBT 函数的定义如下:
func PrintBT(n *Node) {
if n != nil {
fmt.Printf("%v", n.Data)
if n.Left != nil || n.Right != nil {
fmt.Printf("(")
PrintBT(n.Left)
if n.Right != nil {
fmt.Printf(",")
}
PrintBT(n.Right)
fmt.Printf(")")
}
}
}
3) Depth 函数
Depth() 用于计算二叉树的深度,采用递归算法:- 若一棵二叉树为空,则其深度为 0;
- 否则,其深度等于左子树或右子树的最大深度加 1。
Depth 函数的定义如下:
func Depth(n *Node) int {
var depleft, depright int
if n == nil {
return 0
} else {
depleft = Depth(n.Left)
depright = Depth(n.Right)
if depleft > depright {
return depleft + 1
} else {
return depright + 1
}
}
}
4) LeafCount 函数
LeafCount() 用于统计二叉树叶子节点数,采用递归算法:- 若一棵二叉树为空,则其叶子节点数为 0;
- 若一棵二叉树的左、右子树均为空,则其叶子节点数为 1;
- 否则叶子数等于左子树与右子树叶子总数之和。
LeafCount 函数的定义如下:
func LeafCount(n *Node) int {
if n == nil {
return 0
} else if (n.Left == nil) && (n.Right == nil) {
return 1
} else {
return (LeafCount(n.Left) + LeafCount(n.Right))
}
}
5) PreOrder 函数
PreOrder() 可以对二叉树进行前序遍历,采用递归算法,按照先访问根节点,再访问左子树,最后访问右子树的次序访问二叉树中的所有节点,且每个节点仅访问一次。PreOrder 函数的定义如下:
func PreOrder(n *Node) {
if n != nil {
fmt.Printf("%v", n.Data)
PreOrder(n.Left)
PreOrder(n.Right)
}
}
6) InOrder 函数
InOrder() 可以对二叉树进行中序遍历,采用递归算法,按照先访问左子树,再访问根节点,最后访问右子树的次序访问二叉树中的所有节点,且每个节点仅访问一次。InOrder 函数的定义如下:
func InOrder(n *Node) {
if n != nil {
PreOrder(n.Left)
fmt.Printf("%v", n.Data)
PreOrder(n.Right)
}
}
7) PostOrder 函数
PostOrder() 可以对二叉树进行后序遍历,采用递归算法,按照先访问左子树,再访问右子树,最后访问根节点的次序访问二叉树中的所有节点,且每个节点仅访问一次。PostOrder 函数的定义如下:
func PostOrder(n *Node) {
PreOrder(n.Left)
PreOrder(n.Right)
fmt.Printf("%v", n.Data)
}
二叉树基本应用测试
前面介绍了二叉树链接存储结构,以及节点定义、接口定义、方法实现和底层函数设计,并在包 btree 中实现。接下来将利用这些知识实现几个二叉树的基本应用,包括二叉树的创建、基本操作和遍历。二叉树创建
二叉树的创建过程一般如下:- 首先调用 NewNode() 函数创建根节点,再调用 SetData() 方法初始化根节点。
- 使用同样的方法创建左子树和右子树,并将左、右子树链接到根节点上。
- 如果左、右子树有叶子节点,则插入叶子节点并和左、右子树建立链接。
【示例 1】二叉树的建立,本例将演示如何使用 Initer 接口实现根节点的初始化。
// 二叉树的建立
package main
import(
"fmt"
"btree"
)
func main() {
//创建根节点
root := NewNode(nil, nil)
var it Initer
it = root
it.SetData("root node")
//创建左子树
a := NewNode(nil, nil)
a.SetData("left node")
al := NewNode(nil, nil) //左叶子节点
al.SetData(100)
ar := NewNode(nil, nil) //右叶子节点
ar.SetData(3.14)
a.Left = al
a.Right = ar
//创建右子树
b := NewNode(nil, nil)
b.SetData("right node")
root.Left = a
root.Right = b
root.PrintBT()
}
编译并运行该程序,输出结果为:root node (left node ( 100,3.14 ),right node)
通过输出结果可以看出,在示例中首先创建了根节点 root node,然后创建左子树 left node 和右子树 right node。左子树有两个叶子节点,左叶子的值为 int 型 "100",右叶子的值为 float 型 "3.14"。即该二叉树可以存储不同类型的值,这些都是由空接口 interface{} 实现的。二叉树基本操作
对一个已存在的二叉树的基本操作包括二叉树的输出、深度计算、叶子数统计等,在下面将演示如何使用 Operater 接口实现这些基本操作。【示例 2】二叉树的基本操作。
// 二叉树的基本操作
package main
import(
"fmt"
"btree"
)
func main() {
//创建二叉树
root := NewNode(nil, nil)
root.SetData("root node")
a := NewNode(nil, nil)
a.SetData("left node")
al := NewNode(nil, nil)
al.SetData(100)
ar := NewNode(nil, nil)
ar.SetData(3.14)
a.Left = al
a.Right = ar
b := NewNode(nil, nil)
b.SetData("right node")
root.Left = a
root.Right = b
// 使用 Operater 接口实现对二叉树的基本操作
var it Operater
it = root
it.PrintBT()
fmt.Println()
fmt.Println("The depths of the Btree is:", it.Depth())
fmt.Println("The leaf counts of the Btree is:", it.LeafCount())
}
编译并运行该程序,输出结果为:
root node ( left node (100,3.14),right node )
The depths of the Btree is: 3
The leaf counts of the Btree is: 3
二叉树遍历
在二叉树的一些基本应用中,常常需要在树中查找具有某种特征的节点,或者对树中全部节点逐一进行某种处理,这就是二叉树的遍历(Traversing binary tree)。即如何按某条搜索路径访问树中的每个节点,使得每个节点均能被访问一次,而且仅被访问一次。二叉树的遍历方法一般分为前序遍历、中序遍历和后序遍历,下面示例将演示如何使用 Order 接口实现二叉树的三种遍历。
【示例 3】二叉树的遍历。
// 二叉树的遍历
package main
import(
"fmt"
"btree"
)
func main() {
//创建二叉树
root := NewNode(nil, nil)
root.SetData("root node")
a := NewNode(nil, nil)
a.SetData("left node")
al := NewNode(nil, nil)
al.SetData(100)
ar := NewNode(nil, nil)
ar.SetData(3.14)
a.Left = al
a.Right = ar
b := NewNode(nil, nil)
b.SetData("right node")
root.Left = a
root.Right = b
// 使用 Order 接口实现对二叉树的基本操作
var it Order
it = root
it.PreOrder() //先序遍历
fmt.Println()
it.InOrder() //中序遍历
fmt.Println()
it.PostOrder() //后序遍历
}
编译并运行该程序,输出结果为:
root node left node 100 3.14 right node
left node 100 3.14 root node right node
left node 100 3.14 right node root node
所有教程
- C语言入门
- C语言编译器
- C语言项目案例
- 数据结构
- C++
- STL
- C++11
- socket
- GCC
- GDB
- Makefile
- OpenCV
- Qt教程
- Unity 3D
- UE4
- 游戏引擎
- Python
- Python并发编程
- TensorFlow
- Django
- NumPy
- Linux
- Shell
- Java教程
- 设计模式
- Java Swing
- Servlet
- JSP教程
- Struts2
- Maven
- Spring
- Spring MVC
- Spring Boot
- Spring Cloud
- Hibernate
- Mybatis
- MySQL教程
- MySQL函数
- NoSQL
- Redis
- MongoDB
- HBase
- Go语言
- C#
- MATLAB
- JavaScript
- Bootstrap
- HTML
- CSS教程
- PHP
- 汇编语言
- TCP/IP
- vi命令
- Android教程
- 区块链
- Docker
- 大数据
- 云计算