页面置换算法及其优缺点详解
本节,讨论几种页面置换算法。为此,假设有 3 个帧并且引用串为:
注意,并不需要记录调入页面的确切时间,可以创建一个 FIFO 队列,来管理所有的内存页面。置换的是队列的首个页面。当需要调入页面到内存时,就将它加到队列的尾部。
对于样例引用串,3 个帧开始为空。首次的 3 个引用(7,0,1)会引起缺页错误,并被调到这些空帧。之后将调入这些空闲帧。
下一个引用(2)置换 7,这是因为页面 7 最先调入。由于 0 是下一个引用并且已在内存中,所以这个引用不会有缺页错误。
对 3 的首次引用导致页面 0 被替代,因为它现在是队列的第一个。因为这个置换,下一个对 0 的引用将有缺页错误,然后页面1被页面0置换。该进程按图 1 所示方式继续进行。每当有缺页错误时,图 1 显示了哪些页面在这三个帧中。总共有 15 次缺页错误。
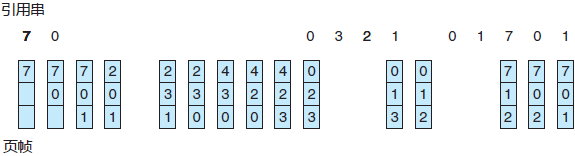
图 1 FIFO页面置换算法
FIFO 页面置换算法易于理解和编程。然而,它的性能并不总是十分理想。一方面,所置换的页面可以是很久以前使用过但现已不再使用的初始化模块。另一方面,所置换的页面可以包含一个被大量使用的变量,它早就初始化了,但仍在不断使用。
注意,即使选择正在使用的一个页面来置换,一切仍然正常工作。在活动页面被置换为新页面后,几乎立即发生缺页错误,以取回活动页面。某个其他页面必须被置换,以便将活动页面调回到内存。因此,选择不当的置换增加缺页错误率,并且减慢处理执行。然而,它不会造成执行不正确。
为了说明使用 FIFO 页面置换算法可能出现的问题,假设如下引用串:
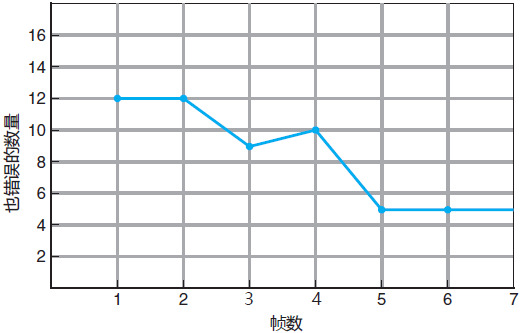
图 2 一个引用串的FIFO置换的缺页错误曲线
这种页面置换算法确保对于给定数量的帧会产生最低的可能的缺页错误率。
例如,针对示例引用串,最优置换算法会产生 9 个缺页错误,如图 3 所示。
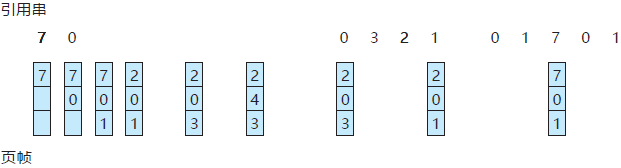
图 3 最优置换算法
头 3 个引用会产生缺页错误,以填满 3 个空闲帧。对页面 2 的引用会置换页面 7,因为页面 7 直到第 18 次引用时才使用,页面 0 在第 5 次引用时使用,页面 1 在第 14 次引用时使用。对页面 3 的引用会置换页面 1,因为页面 1 是位于内存的 3 个页面中最后被再次引用的页面。
有 9 个缺页错误的最优页面置换算法要好于有 15 个缺页错误的 FIFO 置换算法(如果我们忽略前 3 个,这是所有算法都会遭遇的,那么最优置换要比 FIFO 置换好一倍)。事实上,没有置换算法能够只用 3 个侦并且少于 9 个缺页错误,就能处理样例引用串。
然而,最优置换算法难以实现,因为需要引用串的未来知识。因此,最优算法主要用于比较研究。例如,如果知道一个算法不是最优,但是与最优相比最坏不差于 12.3%,平均不差于 4.7%,那么也是很有用的。
如果我们使用最近的过去作为不远将来的近似,那么可以置换最长时间没有使用的页。这种方法称为最近最少使用算法。
LRU 置换将每个页面与它的上次使用的时间关联起来。当需要置换页面时,LRU选择最长时间没有使用的页面。这种策略可当作在时间上向后看而不是向前看的最优页面置换算法。
奇怪的是,如果 SR 表示引用串 S 的倒转,那么针对 S 的 OPT 算法的缺页错误率与针对 SR 的 OPT 算法的缺页错误率是相同的。类似地,针对 S 的 LRU 算法的缺页错误率与针对 SR 的 LRU 算法的缺页错误率相同。
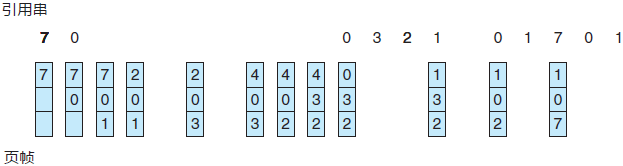
图 4 LRU页面置换算法
将 LRU 置换应用于样例引用串的结果,如图 4 所示。LRU 算法产生 12 次缺页错误。 注意,头 5 个缺页错误与最优置换一样。然而,当页面 4 的引用出现时,由于在内存的 3 个帧中,页面 2 最近最少使用,因此,LRU 算法置换页面 2,而并不知道页面 2 即将要用。
接着,当页面 2 出错时,LRU 算法置换页面 3,因为位于内存的 3 个页中,页面 3 最近最少使用。尽管会有这些问题,有 12 个缺页错误的 LRU 置换仍然要好于有 15 个缺页错误的 FIFO 置换。
LRU 策略通常用作页面置换算法,并被认为是不错的策略。它的主要问题是如何实现 LRU 置换。LRU 页面置换算法可能需要重要的硬件辅助。它的问题是,确定由上次使用时间定义的帧的顺序。两个实现是可行的。
第一种方法是使用计数器:在最简单的情况下,为每个页表条目关联一个使用时间域,并为 CPU 添加一个逻辑时钟或计数器。每次内存引用都会递增时钟。每当进行页面引用时,时钟寄存器的内容会复制到相应页面的页表条目的使用时间域。
这样,我们总是有每个页面的最后引用的“时间”,我们置换具有最小时间的页面。这种方案需要搜索页表以查找 LRU 页面,而且每次内存访问都要写到内存(到页表的使用时间域)。当页表更改时(由于 CPU 调度),还必须保留时间。时钟溢出也要考虑。
实现 LRU 置换的另一种方法是采用页码堆栈。每当页面被引用时,它就从堆栈中移除并放在顶部。这样,最近使用的页面总是在堆栈的顶部,最近最少使用的页面总是在底部(图 5)。因为必须从堆栈的中间删除条目,所以最好通过使用具有首指针和尾指针的双向链表来实现这种方法。
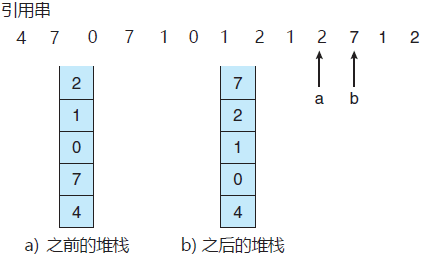
图 5 采用堆栈记录最近页面引用
这样,删除一个页面并放在堆栈顶部,在最坏情况下需要改变 6 个指针。虽说每次更新有点费时,但是置换不需要搜索;指针指向堆栈的底部,这是 LRU 页面。这种方法特别适用于 LRU 置换的软件或微代码实现。
像最优置换一样,LRU 置换没有 Belady 异常。这两个都属于同一类算法,称为堆栈算法,都绝不可能有 Belady 异常。
堆找算法可以证明,帧数为 w 的内存页面集合是帧数为 n+1 的内存页面集合的子集。对于 LRU 置换,内存中的页面集合为最近引用的个页面。如果帧数增加,那么这 n 个页面仍然是最近被引用的,因此仍然在内存中。
注意,除了标准的 TLB 寄存器没有其他辅助硬件,这两种 LRU 实现都是不可能的。每次内存引用,都应更新时钟域或堆栈。如果每次引用都釆用中断以便允许软件更新这些数据结构,那么它会使内存引用至少慢 10 倍,进而使用户进程运行慢 10 倍。很少有系统可以容忍这种级别的内存管理开销。
然而,许多系统都通过引用位的形式提供一定的支持。每当引用一个页面时(无论是对页面的字节进行读或写),它的页面引用位就被硬件置位。页表内的每个条目都关联着一个引用位。
最初,所有引用位由操作系统清零(至 0)。当用户进程执行时,每个引用到的页面引用位由硬件设置(至 1)。一段时间后,我们可以通过检查引用位来确定哪些页面已被使用,哪些页面尚未使用,虽说我们不知道使用的顺序。这种信息是许多近似 LRU 页面置换算法的基础。
例如,如果移位寄存器包含
如果将这些 8 位字节解释为无符号整数,那么具有最小编号的页面是 LRU 页面,可以被替换。请注意,不能保证数字是唯一的。可以置换所有具有最小值的页面,或者在这些页面之间采用 FIFO 来选择置换。
当然,移位寄存器的历史位数可以改变,并可以选择以便使更新尽可能快(取决于可用的硬件)。在极端情况下,位数可降为 0,即只有引用位本身。这种算法称为第二次机会页面置换算法。
当一个页面获得第二次机会时,其引用位被清除,并且到达时间被设为当前时间。因此,获得第二次机会的页面,在所有其他页面被置换(或获得第二次机会)之前,不会被置换。此外,如果一个页面经常使用以致于其引用位总是得到设置,那么它就不会被置换。
实现第二次机会算法(有时称为时钟算法)的一种方式是采用循环队列。指针(即时钟指针)指示接下来要置换哪个页面。当需要一个帧时,指针向前移动直到找到一个引用位为 0 的页面。在向前移动时,它会清除引用位(图 6)。一旦找到牺牲页面,就置换该页面,并且在循环队列的这个位置上插入新页面。
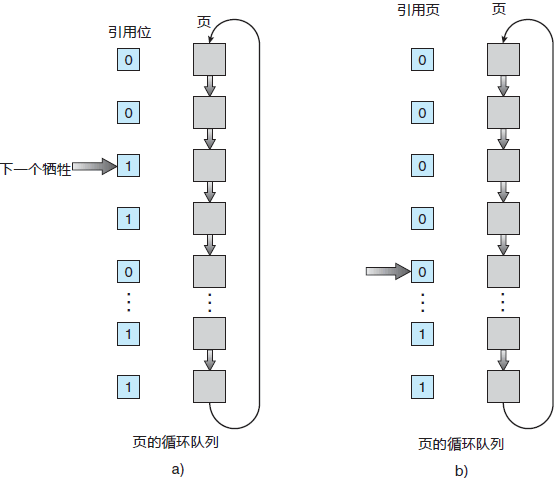
图 6 第二次机会(时钟)页面置换算法
注意,在最坏的情况下,当所有位都已设置,指针会循环遍历整个队列,给每个页面第二次机会。在选择下一个页面进行置换之前,它将清除所有引用位。如果所有位都为 1,第二次机会置换退化为 FIFO 替换。
每个页面都属于这四种类型之一。当需要页面置换时,可使用与时钟算法一样的方案;但不是检查所指页面的引用位是否设置,而是检查所查页面属于哪个类型。我们替换非空的最低类型中的第一个页面。请注意,可能需要多次扫描循环队列,才会找到要置换的页面。
这种算法与更为简单的时钟算法的主要区别在于:这里为那些已修改页面赋予更高级别,从而降低了所需 I/O 数量。
正如你可以想象的,MFU 和 LFU 置换都不常用。这些算法的实现是昂贵的,并且它们不能很好地近似 OPT 置换。
这种方法的扩展之一是维护一个修改页面的列表。每当调页设备空闲时,就选择一个修改页面以写到磁盘上,然后重置它的修改位。这种方案增加了在需要选择置换时干净的且无需写出的页面的概率。
另一种修改是保留一个空闲帧池,并且记住哪些页面在哪些帧内。因为在帧被写到磁盘后帧内容并未被修改,所以当该帧被重用之前,如果再次需要,那么旧的页面可以从空闲帧池中直接取出并被使用。这种情况不需要 I/O。当发生缺页错误时,首先检查所需页面是否在空闲帧池中。如果不在,我们应选择一个自由侦并读入页面。
这种技术与 FIFO 置换算法一起用于 VAX/VMS 系统中。当 FIFO 置换算法错误地置换了一个常用页面时,该页面可从空闲帧池中很快取出,而且不需要 I/O。这种空闲帧缓冲弥补了相对差但却简单的 FIFO 置换算法。这种方法是必要的,因为早期版本的 VAX 没有正确实现引用位。
有些版本的 UNIX 系统将此方法与第二次机会算法一起使用。这种方法可用来改进任何页面置换算法,以降低因错误选择牺牲页面而引起的开销。
另一个例子是数据仓库,它频繁地执行大量的、顺序的磁盘读取,随后计算并写入。LRU 算法会删除旧的页面并保留新的页面,而应用程序将更可能读取较旧的页面而不是较新的页面(因为它再次开始顺序读取)。这里,MFU 可能比 LRU 更为高效。
由于这些问题,有的操作系统允许特殊程序能够将磁盘分区作为逻辑块的大的数组来使用,而不需要通过文件系统的数据结构。这种数组有时称为原始磁盘,而这种数组的 I/O 称为原始 I/O。
原始 I/O 绕过所有文件系统服务,例如文件 I/O 的请求调页、文件锁定、预取、空间分配、文件名和目录等。请注意,尽管有些应用程序在原始分区上实现自己的专用存储服务更加高效,但是大多数应用程序采用通用文件系统服务更好。
7,0,1,2,0,3,0,4,2,3,0,3,2,1,2,0,1,7,0,1
FIFO页面置换
FIFO 算法是最简单的页面置换算法。FIFO 页面置换算法为每个页面记录了调到内存的时间,当必须置换页面时会选择最旧的页面。注意,并不需要记录调入页面的确切时间,可以创建一个 FIFO 队列,来管理所有的内存页面。置换的是队列的首个页面。当需要调入页面到内存时,就将它加到队列的尾部。
对于样例引用串,3 个帧开始为空。首次的 3 个引用(7,0,1)会引起缺页错误,并被调到这些空帧。之后将调入这些空闲帧。
下一个引用(2)置换 7,这是因为页面 7 最先调入。由于 0 是下一个引用并且已在内存中,所以这个引用不会有缺页错误。
对 3 的首次引用导致页面 0 被替代,因为它现在是队列的第一个。因为这个置换,下一个对 0 的引用将有缺页错误,然后页面1被页面0置换。该进程按图 1 所示方式继续进行。每当有缺页错误时,图 1 显示了哪些页面在这三个帧中。总共有 15 次缺页错误。

图 1 FIFO页面置换算法
FIFO 页面置换算法易于理解和编程。然而,它的性能并不总是十分理想。一方面,所置换的页面可以是很久以前使用过但现已不再使用的初始化模块。另一方面,所置换的页面可以包含一个被大量使用的变量,它早就初始化了,但仍在不断使用。
注意,即使选择正在使用的一个页面来置换,一切仍然正常工作。在活动页面被置换为新页面后,几乎立即发生缺页错误,以取回活动页面。某个其他页面必须被置换,以便将活动页面调回到内存。因此,选择不当的置换增加缺页错误率,并且减慢处理执行。然而,它不会造成执行不正确。
为了说明使用 FIFO 页面置换算法可能出现的问题,假设如下引用串:
1,2,3,4,1,2,5,1,2,3,4,5
图 2 为这个引用串的缺页错误数量与可用帧数量的曲线。4 帧的缺页错误数(10)比 3 帧的缺页错误数(9)还要大!这个最意想不到的结果被称为 Belady 异常,即对于有些页面置换算法,随着分配帧数量的增加,缺页错误率可能会增加,虽然我们原本期望为一个进程提供更多的内存可以改善其性能。
图 2 一个引用串的FIFO置换的缺页错误曲线
最优页面置换
发现 Belady 异常的一个结果是寻找最优页面置换算法,这个算法具有所有算法的最低的缺页错误率,并且不会遭受 Belady 异常。这种算法确实存在,它被称为 OPT 或 MIN。该算法的思想是:置换最长时间不会使用的页面。这种页面置换算法确保对于给定数量的帧会产生最低的可能的缺页错误率。
例如,针对示例引用串,最优置换算法会产生 9 个缺页错误,如图 3 所示。

图 3 最优置换算法
头 3 个引用会产生缺页错误,以填满 3 个空闲帧。对页面 2 的引用会置换页面 7,因为页面 7 直到第 18 次引用时才使用,页面 0 在第 5 次引用时使用,页面 1 在第 14 次引用时使用。对页面 3 的引用会置换页面 1,因为页面 1 是位于内存的 3 个页面中最后被再次引用的页面。
有 9 个缺页错误的最优页面置换算法要好于有 15 个缺页错误的 FIFO 置换算法(如果我们忽略前 3 个,这是所有算法都会遭遇的,那么最优置换要比 FIFO 置换好一倍)。事实上,没有置换算法能够只用 3 个侦并且少于 9 个缺页错误,就能处理样例引用串。
然而,最优置换算法难以实现,因为需要引用串的未来知识。因此,最优算法主要用于比较研究。例如,如果知道一个算法不是最优,但是与最优相比最坏不差于 12.3%,平均不差于 4.7%,那么也是很有用的。
LRU页面置换
如果最优算法不可行,那么最优算法的近似或许成为可能。FIFO 和 OPT 算法的关键区别在于,除了在时间上向后或向前看之外,FIFO 算法使用的是页面调入内存的时间,OPT 算法使用的是页面将来使用的时间。如果我们使用最近的过去作为不远将来的近似,那么可以置换最长时间没有使用的页。这种方法称为最近最少使用算法。
LRU 置换将每个页面与它的上次使用的时间关联起来。当需要置换页面时,LRU选择最长时间没有使用的页面。这种策略可当作在时间上向后看而不是向前看的最优页面置换算法。
奇怪的是,如果 SR 表示引用串 S 的倒转,那么针对 S 的 OPT 算法的缺页错误率与针对 SR 的 OPT 算法的缺页错误率是相同的。类似地,针对 S 的 LRU 算法的缺页错误率与针对 SR 的 LRU 算法的缺页错误率相同。

图 4 LRU页面置换算法
将 LRU 置换应用于样例引用串的结果,如图 4 所示。LRU 算法产生 12 次缺页错误。 注意,头 5 个缺页错误与最优置换一样。然而,当页面 4 的引用出现时,由于在内存的 3 个帧中,页面 2 最近最少使用,因此,LRU 算法置换页面 2,而并不知道页面 2 即将要用。
接着,当页面 2 出错时,LRU 算法置换页面 3,因为位于内存的 3 个页中,页面 3 最近最少使用。尽管会有这些问题,有 12 个缺页错误的 LRU 置换仍然要好于有 15 个缺页错误的 FIFO 置换。
LRU 策略通常用作页面置换算法,并被认为是不错的策略。它的主要问题是如何实现 LRU 置换。LRU 页面置换算法可能需要重要的硬件辅助。它的问题是,确定由上次使用时间定义的帧的顺序。两个实现是可行的。
第一种方法是使用计数器:在最简单的情况下,为每个页表条目关联一个使用时间域,并为 CPU 添加一个逻辑时钟或计数器。每次内存引用都会递增时钟。每当进行页面引用时,时钟寄存器的内容会复制到相应页面的页表条目的使用时间域。
这样,我们总是有每个页面的最后引用的“时间”,我们置换具有最小时间的页面。这种方案需要搜索页表以查找 LRU 页面,而且每次内存访问都要写到内存(到页表的使用时间域)。当页表更改时(由于 CPU 调度),还必须保留时间。时钟溢出也要考虑。
实现 LRU 置换的另一种方法是采用页码堆栈。每当页面被引用时,它就从堆栈中移除并放在顶部。这样,最近使用的页面总是在堆栈的顶部,最近最少使用的页面总是在底部(图 5)。因为必须从堆栈的中间删除条目,所以最好通过使用具有首指针和尾指针的双向链表来实现这种方法。

图 5 采用堆栈记录最近页面引用
这样,删除一个页面并放在堆栈顶部,在最坏情况下需要改变 6 个指针。虽说每次更新有点费时,但是置换不需要搜索;指针指向堆栈的底部,这是 LRU 页面。这种方法特别适用于 LRU 置换的软件或微代码实现。
像最优置换一样,LRU 置换没有 Belady 异常。这两个都属于同一类算法,称为堆栈算法,都绝不可能有 Belady 异常。
堆找算法可以证明,帧数为 w 的内存页面集合是帧数为 n+1 的内存页面集合的子集。对于 LRU 置换,内存中的页面集合为最近引用的个页面。如果帧数增加,那么这 n 个页面仍然是最近被引用的,因此仍然在内存中。
注意,除了标准的 TLB 寄存器没有其他辅助硬件,这两种 LRU 实现都是不可能的。每次内存引用,都应更新时钟域或堆栈。如果每次引用都釆用中断以便允许软件更新这些数据结构,那么它会使内存引用至少慢 10 倍,进而使用户进程运行慢 10 倍。很少有系统可以容忍这种级别的内存管理开销。
近似LRU页面置换
很少有计算机系统能提供足够的硬件来支持真正的 LRU 页面置换算法。事实上,有些系统不提供硬件支持,并且必须使用其他页面置换算法(例如 FIFO 算法)。然而,许多系统都通过引用位的形式提供一定的支持。每当引用一个页面时(无论是对页面的字节进行读或写),它的页面引用位就被硬件置位。页表内的每个条目都关联着一个引用位。
最初,所有引用位由操作系统清零(至 0)。当用户进程执行时,每个引用到的页面引用位由硬件设置(至 1)。一段时间后,我们可以通过检查引用位来确定哪些页面已被使用,哪些页面尚未使用,虽说我们不知道使用的顺序。这种信息是许多近似 LRU 页面置换算法的基础。
额外引用位算法
通过定期记录引用位,我们可以获得额外的排序信息。可以为内存中的页表的每个页面保留一个 8 位的字节。定时器中断定期地(如每 100ms)将控制传到操作系统。操作系统将每个页面引用位移到其 8 位字节的高位,将其他位右移 1 位,并丢弃最低位。这些 8 位移位寄存器包含着最近 8 个时间周期内的页面使用情况。例如,如果移位寄存器包含
00000000,那么该页面在 8 个时间周期内没有使用。每个周期内使用至少一次的页面具有 11111111 的移位寄存器值。具有 11000100 的历史寄存器值的页面比具有值为 01110111 的页面更为“最近使用的”。如果将这些 8 位字节解释为无符号整数,那么具有最小编号的页面是 LRU 页面,可以被替换。请注意,不能保证数字是唯一的。可以置换所有具有最小值的页面,或者在这些页面之间采用 FIFO 来选择置换。
当然,移位寄存器的历史位数可以改变,并可以选择以便使更新尽可能快(取决于可用的硬件)。在极端情况下,位数可降为 0,即只有引用位本身。这种算法称为第二次机会页面置换算法。
第二次机会算法
第二次机会置换的基本算法是一种 FIFO 置换算法。然而,当选择了一个页面时,需要检查其引用位。如果值为 0,那么就直接置换此页面;如果引用位设置为 1,那么就给此页面第二次机会,并继续选择下一个 FIFO 页面。当一个页面获得第二次机会时,其引用位被清除,并且到达时间被设为当前时间。因此,获得第二次机会的页面,在所有其他页面被置换(或获得第二次机会)之前,不会被置换。此外,如果一个页面经常使用以致于其引用位总是得到设置,那么它就不会被置换。
实现第二次机会算法(有时称为时钟算法)的一种方式是采用循环队列。指针(即时钟指针)指示接下来要置换哪个页面。当需要一个帧时,指针向前移动直到找到一个引用位为 0 的页面。在向前移动时,它会清除引用位(图 6)。一旦找到牺牲页面,就置换该页面,并且在循环队列的这个位置上插入新页面。

图 6 第二次机会(时钟)页面置换算法
注意,在最坏的情况下,当所有位都已设置,指针会循环遍历整个队列,给每个页面第二次机会。在选择下一个页面进行置换之前,它将清除所有引用位。如果所有位都为 1,第二次机会置换退化为 FIFO 替换。
增强型第二次机会算法
通过将引用位和修改位作为有序对,可以改进二次机会算法。有了这两个位,就有下面四种可能的类型:- (0,0):最近没有使用且没有修改的页面,最佳的页面置换。
- (0,1):最近没有使用但修改过的页面,不太好的置换,因为在置换之前需要将页面写出。
- (1,0):最近使用过但没有修改的页面,可能很快再次使用。
- (1,1):最近使用过且修改过,可能很快再次使用,并且在置换之前需要将页面写出到磁盘。
每个页面都属于这四种类型之一。当需要页面置换时,可使用与时钟算法一样的方案;但不是检查所指页面的引用位是否设置,而是检查所查页面属于哪个类型。我们替换非空的最低类型中的第一个页面。请注意,可能需要多次扫描循环队列,才会找到要置换的页面。
这种算法与更为简单的时钟算法的主要区别在于:这里为那些已修改页面赋予更高级别,从而降低了所需 I/O 数量。
基于计数的页面置换
页面置换还有许多其他算法。例如,可以为每个页面的引用次数保存一个计数器,并且开发以下两个方案。- 最不经常使用(LFU)页面置换算法要求置换具有最小计数的页面。这种选择的原因是,积极使用的页面应当具有大的引用计数。然而,当一个页面在进程的初始阶段大量使用但是随后不再使用时,会出现问题。由于被大量使用,它有一个大的计数,即使不再需要却仍保留在内存中。一种解决方案是,定期地将计数右移 1 位,以形成指数衰减的平均使用计数。
- 最经常使用(MFU)页面置换算法是基于如下论点:具有最小计数的页面可能刚刚被引入并且尚未使用。
正如你可以想象的,MFU 和 LFU 置换都不常用。这些算法的实现是昂贵的,并且它们不能很好地近似 OPT 置换。
页面缓冲算法
除了特定页面置换算法之外,还经常采用其他措施。例如,系统通常保留一个空闲帧缓冲池。当出现缺页错误时,会像以前一样选择一个牺牲帧。然而,在写出牺牲帧之前,所需页面就读到来自缓冲池的空闲帧。这种措施允许进程尽快重新启动,而无需等待写出牺牲帧。当牺牲帧以后被写出后,它被添加到空闲帧池。这种方法的扩展之一是维护一个修改页面的列表。每当调页设备空闲时,就选择一个修改页面以写到磁盘上,然后重置它的修改位。这种方案增加了在需要选择置换时干净的且无需写出的页面的概率。
另一种修改是保留一个空闲帧池,并且记住哪些页面在哪些帧内。因为在帧被写到磁盘后帧内容并未被修改,所以当该帧被重用之前,如果再次需要,那么旧的页面可以从空闲帧池中直接取出并被使用。这种情况不需要 I/O。当发生缺页错误时,首先检查所需页面是否在空闲帧池中。如果不在,我们应选择一个自由侦并读入页面。
这种技术与 FIFO 置换算法一起用于 VAX/VMS 系统中。当 FIFO 置换算法错误地置换了一个常用页面时,该页面可从空闲帧池中很快取出,而且不需要 I/O。这种空闲帧缓冲弥补了相对差但却简单的 FIFO 置换算法。这种方法是必要的,因为早期版本的 VAX 没有正确实现引用位。
有些版本的 UNIX 系统将此方法与第二次机会算法一起使用。这种方法可用来改进任何页面置换算法,以降低因错误选择牺牲页面而引起的开销。
应用程序与页面置换
在某些情况下,通过操作系统的虚拟内存访问数据的应用程序比操作系统根本没有提供缓冲区更差。一个典型的例子是数据库,它提供自己的内存管理和 I/O 缓冲。类似这样的程序比提供通用目的算法的操作系统,更能理解自己的内存使用与磁盘使用。如果操作系统提供 I/O 缓冲而应用程序也提供 I/O 缓冲,那么用于这些 I/O 的内存自然就成倍了。另一个例子是数据仓库,它频繁地执行大量的、顺序的磁盘读取,随后计算并写入。LRU 算法会删除旧的页面并保留新的页面,而应用程序将更可能读取较旧的页面而不是较新的页面(因为它再次开始顺序读取)。这里,MFU 可能比 LRU 更为高效。
由于这些问题,有的操作系统允许特殊程序能够将磁盘分区作为逻辑块的大的数组来使用,而不需要通过文件系统的数据结构。这种数组有时称为原始磁盘,而这种数组的 I/O 称为原始 I/O。
原始 I/O 绕过所有文件系统服务,例如文件 I/O 的请求调页、文件锁定、预取、空间分配、文件名和目录等。请注意,尽管有些应用程序在原始分区上实现自己的专用存储服务更加高效,但是大多数应用程序采用通用文件系统服务更好。
所有教程
- C语言入门
- C语言编译器
- C语言项目案例
- 数据结构
- C++
- STL
- C++11
- socket
- GCC
- GDB
- Makefile
- OpenCV
- Qt教程
- Unity 3D
- UE4
- 游戏引擎
- Python
- Python并发编程
- TensorFlow
- Django
- NumPy
- Linux
- Shell
- Java教程
- 设计模式
- Java Swing
- Servlet
- JSP教程
- Struts2
- Maven
- Spring
- Spring MVC
- Spring Boot
- Spring Cloud
- Hibernate
- Mybatis
- MySQL教程
- MySQL函数
- NoSQL
- Redis
- MongoDB
- HBase
- Go语言
- C#
- MATLAB
- JavaScript
- Bootstrap
- HTML
- CSS教程
- PHP
- 汇编语言
- TCP/IP
- vi命令
- Android教程
- 区块链
- Docker
- 大数据
- 云计算