STL priority_queue底层实现(深度剖析)
priority_queue 优先级队列之所以总能保证优先级最高的元素位于队头,最重要的原因是其底层采用堆数据结构存储结构。
有读者可能会问,priority_queue 底层不是采用 vector 或 deque 容器存储数据吗,这里又说使用堆结构存储数据,它们之间不冲突吗?显然,它们之间是不冲突的。
首先,vector 和 deque 是用来存储元素的容器,而堆是一种数据结构,其本身无法存储数据,只能依附于某个存储介质,辅助其组织数据存储的先后次序。其次,priority_queue 底层采用 vector 或者 deque 作为基础容器,这毋庸置疑。但由于 vector 或 deque 容器并没有提供实现 priority_queue 容器适配器 “First in,Largest out” 特性的功能,因此 STL 选择使用堆来重新组织 vector 或 deque 容器中存储的数据,从而实现该特性。
图 1 展示了一个由
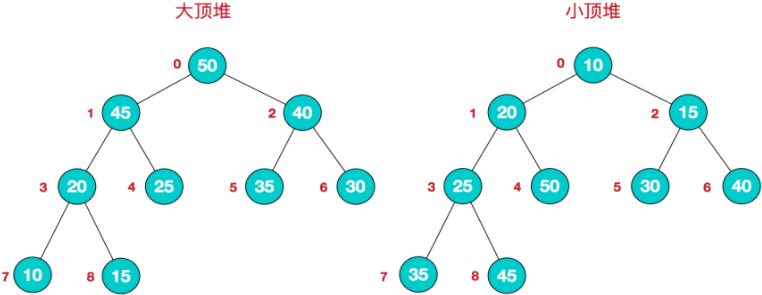
图 1 使用堆结构重新组织数据
可以看到,大顶堆中,每个父节点的值都不小于子节点;同样在小顶堆中,每个父节点的值都不大于子节点。但需要注意的是,无论是大顶堆还是小顶堆,同一父节点下子节点的次序是不做规定的,这也是经大顶堆或小顶堆组织后的数据整体依然无序的原因。
可以确定的一点是,无论是通过大顶堆或者小顶堆,总可以筛选出最大或最小的那个元素(优先级最大),并将其移至序列的开头,此功能也正是 priority_queue 容器适配器所需要的。
为了验证 priority_queue 底层确实采用堆存储结构实现的,我们可以尝试用堆结合基础容器 vector 或 deque 实现 priority_queue。值得庆幸的是,STL 已经为我们封装好了可以使用堆存储结构的方法,它们都位于 <algorithm> 头文件中。表 2 中列出了常用的几个和堆存储结构相关的方法。
上面程序可以用 priority_queue 容器适配器等效替代:
有读者可能会问,priority_queue 底层不是采用 vector 或 deque 容器存储数据吗,这里又说使用堆结构存储数据,它们之间不冲突吗?显然,它们之间是不冲突的。
首先,vector 和 deque 是用来存储元素的容器,而堆是一种数据结构,其本身无法存储数据,只能依附于某个存储介质,辅助其组织数据存储的先后次序。其次,priority_queue 底层采用 vector 或者 deque 作为基础容器,这毋庸置疑。但由于 vector 或 deque 容器并没有提供实现 priority_queue 容器适配器 “First in,Largest out” 特性的功能,因此 STL 选择使用堆来重新组织 vector 或 deque 容器中存储的数据,从而实现该特性。
那么,堆到底是什么,它又是怎样组织数据的呢?注意,虽然不使用堆结构,通过编写算法调整 vector 或者 deque 容器中存储元素的次序,也能使其具备 “First in,Largest out” 的特性,但执行效率通常没有使用堆结构高。
priority_queue底层的堆存储结构
简单的理解堆,它在是完全二叉树的基础上,要求树中所有的父节点和子节点之间,都要满足既定的排序规则:以下内容要求读者对数据结构中的树存储结构有一定的了解,如果没有,请先阅读《树存储结构》一章。
- 如果排序规则为从大到小排序,则表示堆的完全二叉树中,每个父节点的值都要不小于子节点的值,这种堆通常称为大顶堆;
- 如果排序规则为从小到大排序,则表示堆的完全二叉树中,每个父节点的值都要不大于子节点的值,这种堆通常称为小顶堆;
图 1 展示了一个由
{10,20,15,30,40,25,35,50,45} 这些元素构成的大顶堆和小顶堆。其中经大顶堆组织后的数据先后次序变为 {50,45,40,20,25,35,30,10,15},而经小顶堆组织后的数据次序为{10,20,15,25,50,30,40,35,45}。

图 1 使用堆结构重新组织数据
可以看到,大顶堆中,每个父节点的值都不小于子节点;同样在小顶堆中,每个父节点的值都不大于子节点。但需要注意的是,无论是大顶堆还是小顶堆,同一父节点下子节点的次序是不做规定的,这也是经大顶堆或小顶堆组织后的数据整体依然无序的原因。
可以确定的一点是,无论是通过大顶堆或者小顶堆,总可以筛选出最大或最小的那个元素(优先级最大),并将其移至序列的开头,此功能也正是 priority_queue 容器适配器所需要的。
为了验证 priority_queue 底层确实采用堆存储结构实现的,我们可以尝试用堆结合基础容器 vector 或 deque 实现 priority_queue。值得庆幸的是,STL 已经为我们封装好了可以使用堆存储结构的方法,它们都位于 <algorithm> 头文件中。表 2 中列出了常用的几个和堆存储结构相关的方法。
| 函数 | 功能 |
|---|---|
| make_heap(first,last,comp) | 选择位于 [first,last) 区域内的数据,并根据 comp 排序规则建立堆,其中 fist 和 last 可以是指针或者迭代器,默认是建立大顶堆。 |
| push_heap(first,last,comp) | 当向数组或容器中添加数据之后,此数据可能会破坏堆结构,该函数的功能是重建堆。 |
| pop_heap(first,last,comp) | 将位于序列头部的元素(优先级最高)移动序列尾部,并使[first,last-1] 区域内的元素满足堆存储结构。 |
| sort_heap(first,last,comp) | 对 [first,last) 区域内的元素进行堆排序,将其变成一个有序序列。 |
| is_heap_until(first,last,comp) | 发现[first,last)区域内的最大堆。 |
| is_heap(first,last,comp) | 检查 [first,last) 区域内的元素,是否为堆结构。 |
下面例子中,使用了表 2 中的部分函数,并结合 vector 容器提供的成员函数,模拟了 priority_queue 容器适配器部分成员函数的底层实现:以上方法的实现,基于堆排序算法的思想,有关该算法的具体实现原理,可阅读《堆排序》一节做详细了解。
#include <iostream> #include <vector> #include<algorithm> using namespace std; void display(vector<int>& val) { for (auto v : val) { cout << v << " "; } cout << endl; } int main() { vector<int>values{ 2,1,3,4 }; //建立堆 make_heap(values.begin(), values.end());//{4,2,3,1} display(values); //添加元素 cout << "添加元素:\n"; values.push_back(5); display(values); push_heap(values.begin(), values.end());//{5,4,3,1,2} display(values); //移除元素 cout << "移除元素:\n"; pop_heap(values.begin(), values.end());//{4,2,3,1,5} display(values); values.pop_back(); display(values); return 0; }运行结果为:
4 2 3 1
添加元素:
4 2 3 1 5
5 4 3 1 2
移除元素:
4 2 3 1 5
4 2 3 1
上面程序可以用 priority_queue 容器适配器等效替代:
#include<iostream>
#include<queue>
#include<vector>
using namespace std;
int main()
{
//创建优先级队列
std::vector<int>values{ 2,1,3,4 };
std::priority_queue<int>copy_values(values.begin(), values.end());
//添加元素
copy_values.push(5);
//移除元素
copy_values.pop();
return 0;
}
如果调试此程序,查看各个阶段 priority_queue 中存储的元素,可以发现,它和上面程序的输出结果是一致。也就是说,此程序在创建 priority_queue 之后,其存储的元素依次为 {4,2,3,1},同样当添加元素 5 之后,其存储的元素依次为 {5,4,3,1,2},移除一个元素之后存储的元素依次为 {4,2,3,1}。 所有教程
- C语言入门
- C语言编译器
- C语言项目案例
- 数据结构
- C++
- STL
- C++11
- socket
- GCC
- GDB
- Makefile
- OpenCV
- Qt教程
- Unity 3D
- UE4
- 游戏引擎
- Python
- Python并发编程
- TensorFlow
- Django
- NumPy
- Linux
- Shell
- Java教程
- 设计模式
- Java Swing
- Servlet
- JSP教程
- Struts2
- Maven
- Spring
- Spring MVC
- Spring Boot
- Spring Cloud
- Hibernate
- Mybatis
- MySQL教程
- MySQL函数
- NoSQL
- Redis
- MongoDB
- HBase
- Go语言
- C#
- MATLAB
- JavaScript
- Bootstrap
- HTML
- CSS教程
- PHP
- 汇编语言
- TCP/IP
- vi命令
- Android教程
- 区块链
- Docker
- 大数据
- 云计算