NumPy的算术运算
在机器学习和深度学习中,涉及大量的数组或矩阵运算,本节我们将重点介绍两种常用的运算:
类似地,
以下我们通过一些示例来进一步说明:
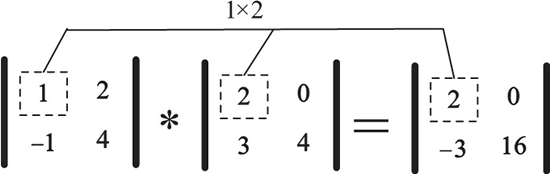
图1:对应元素相乘示意图
NumPy 数组不仅可以和数组进行对应元素相乘,还可以和单一数值(或称为标量)进行运算。运算时,NumPy 数组中的每个元素都和标量进行运算,其间会用到广播机制。
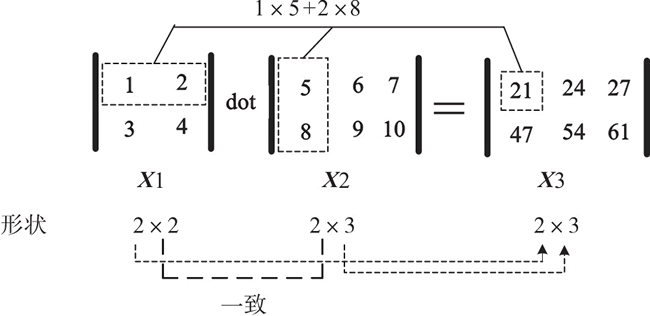
图2:矩阵的点积示意图,对应维度的元素个数需要保持一致
在图2中,矩阵 X1 和矩阵 X2 进行点积运算,其中 X1 和 X2 对应维度(即 X1 的第 2 个维度与 X2 的第 1 个维度)的元素个数必须保持一致。此外,矩阵 X3 的形状是由矩阵 X1 的行数与矩阵 X2 的列数构成的。
-
一种是对应元素相乘,又称为逐元乘法(Element-Wise Product),可以使用 np.multiply() 函数或者
*运算符; - 另一种是点积或内积元素,运算符为 np.dot()。
对应元素相乘
对应元素相乘(Element-Wise Product)是两个矩阵中对应元素乘积。np.multiply() 函数用于数组或矩阵对应元素相乘,输出与相乘数组或矩阵的大小一致,其格式如下:numpy.multiply(x1, x2, /, out=None, *, where=True,casting='same_kind', order='K', dtype=None, subok=True[, signature, extobj])
其中 x1、x2 之间的对应元素相乘遵守广播规则,NumPy 的广播规则后续将会介绍。类似地,
*运算符也能达到同样的效果。以下我们通过一些示例来进一步说明:
>>> A = np.array([[1, 2], [-1, 4]])
>>> B = np.array([[2, 0], [3, 4]])
>>> A*B
array([[ 2, 0],
[-3, 16]])
>>> np.multiply(A, B)
array([[ 2, 0],
[-3, 16]])
矩阵 A 和 B 的对应元素相乘,由图1直观表示。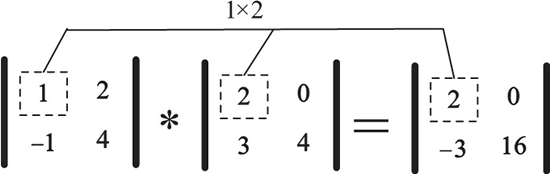
图1:对应元素相乘示意图
NumPy 数组不仅可以和数组进行对应元素相乘,还可以和单一数值(或称为标量)进行运算。运算时,NumPy 数组中的每个元素都和标量进行运算,其间会用到广播机制。
>>> print(A*2.0) [[ 2. 4.] [-2. 8.]] >>> print(A/2.0) [[ 0.5 1. ] [-0.5 2. ]]由此,推而广之,数组通过一些激活函数后,输出与输入形状一致。
X=np.random.rand(2, 3)
def softmoid(x):
return 1/(1+np.exp(-x))
def relu(x):
return np.maximum(0, x)
def softmax(x):
return np.exp(x)/np.sum(np.exp(x))
print("输入参数X的形状:", X.shape)
print("激活函数softmoid输出形状:", softmoid(X).shape)
print("激活函数relu输出形状:", relu(X).shape)
print("激活函数softmax输出形状:", softmax(X).shape)
运行结果:
输入参数X的形状: (2, 3)
激活函数softmoid输出形状: (2, 3)
激活函数relu输出形状: (2, 3)
激活函数softmax输出形状: (2, 3)
点积运算
点积运算(Dot Product)又称为内积,在 NumPy 中用 np.dot() 函数表示,其一般格式为:numpy.dot(a, b, out=None)
以下通过一个示例来说明 dot() 的具体使用方法及注意事项:X1=np.array([[1,2],[3,4]]) X2=np.array([[5,6,7],[8,9,10]]) X3=np.dot(X1,X2) print(X3)输出结果:
[[21 24 27]
[47 54 61]]

图2:矩阵的点积示意图,对应维度的元素个数需要保持一致
在图2中,矩阵 X1 和矩阵 X2 进行点积运算,其中 X1 和 X2 对应维度(即 X1 的第 2 个维度与 X2 的第 1 个维度)的元素个数必须保持一致。此外,矩阵 X3 的形状是由矩阵 X1 的行数与矩阵 X2 的列数构成的。
所有教程
- C语言入门
- C语言编译器
- C语言项目案例
- 数据结构
- C++
- STL
- C++11
- socket
- GCC
- GDB
- Makefile
- OpenCV
- Qt教程
- Unity 3D
- UE4
- 游戏引擎
- Python
- Python并发编程
- TensorFlow
- Django
- NumPy
- Linux
- Shell
- Java教程
- 设计模式
- Java Swing
- Servlet
- JSP教程
- Struts2
- Maven
- Spring
- Spring MVC
- Spring Boot
- Spring Cloud
- Hibernate
- Mybatis
- MySQL教程
- MySQL函数
- NoSQL
- Redis
- MongoDB
- HBase
- Go语言
- C#
- MATLAB
- JavaScript
- Bootstrap
- HTML
- CSS教程
- PHP
- 汇编语言
- TCP/IP
- vi命令
- Android教程
- 区块链
- Docker
- 大数据
- 云计算