C++快速排序(递归)算法详解
快速排序是由 C.A.R.Hoare 于 1962 年发明的递归排序算法。它非常高效,通常用于对存储在数组中的项目列表进行排序。
快速排序通常写成一个包含 3 个形参的递归函数,这 3 个形参可以定义要排序的数组的一部分,它们分别是,一个包含项目列表的数组 arr,以及两个下标 start 和 end,表示要排序的 arr 数组段的开始和结束。可以将这 3 个形参写作 arr[start .. end]。要对整个数组进行排序,可以调用快速排序,将 start 设置为 0,并将 end 设置为数组大小减 1。
快速排序的工作原理如下,如果 start 大于或等于 end,那么被排序的 arr 段最多有一个元素,因此已经排序,在这种情况下,快速排序立即返回。否则,快速排序将通过选择 arr[start .. end] 中的一个元素作为一个基准元素,来对 arr[start .. end] 进行分区,然后重新排列 arr[start .. end],以便所有小于基准的条目都在基准的左侧,所有大于或等于基准的条目都在基准的右侧。
实际上,分区步骤重新排列了 arr[start..end],以使它由子列表 1、基准元素和子列表 2 组成,如图 1 所示。
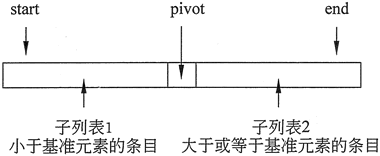
图 1 快速排序以基准元素为中心进行分区
根据选定的基准元素的值,两个子列表中的一个或另一个可能是空的。例如,如果基准元素碰巧是最小数组元素,那么将不会有数组条目小于基准元素,所以子列表 1 将是空的。
请注意,一旦分区阶段完成,则会出现如图 1 所示的情况,基准元素将在正确的位置。通过递归地将快速排序过程应用于两个子列表,每个子列表将被分区,将任何被选择为该子列表的基准元素放置在正确的位置。这个过程一直持续到子列表的长度最多为 1 止。此时,原始数组将被排序。
假设有一个函数如下:
然后即可在 C++ 中实现快速排序,如下所示:
分区的主要思想是按一次一个元素的方式扩展数组分区部分。设想元素 X 刚好位于子列表 2 最右侧,如果这个 X 大于或等于基准元素,则将其添加到子列表 2 的末尾(把它留在原来的位置即可),然后继续考虑下一个元素;如果 X 小于基准元素,则将其添加到子元素 1 的末尾,方法是将其放到基准元素的左侧。
要做到这一点,有一种方式是将 X 存储在临时位置,将子列表 2 中的每个元素向右移动一个位置,将基准元素也向右移动一个位置,然后将 X 放入由基准元素腾出来的数组位置。这种策略虽然简单,但是需要移动太多的数组元素,因此并不是有效的算法。
相反,我们可以更高效地将 X 放置在基准元素的左侧,方法是首先使用 X 与刚好在基准元素右侧的数组项 Y 交换,然后再让 X 与基准元素进行交换。第一次交换将 Y (大于或等于基准元素)置于子列表 2 的末尾,同时将 X 放置在与基准元素相邻的位置;第二次交换则把 X 放在基准元素的左侧。如此重复,直到整个列表已被分区。
执行分区操作的 partition 函数代码如下:
快速排序通常写成一个包含 3 个形参的递归函数,这 3 个形参可以定义要排序的数组的一部分,它们分别是,一个包含项目列表的数组 arr,以及两个下标 start 和 end,表示要排序的 arr 数组段的开始和结束。可以将这 3 个形参写作 arr[start .. end]。要对整个数组进行排序,可以调用快速排序,将 start 设置为 0,并将 end 设置为数组大小减 1。
快速排序的工作原理如下,如果 start 大于或等于 end,那么被排序的 arr 段最多有一个元素,因此已经排序,在这种情况下,快速排序立即返回。否则,快速排序将通过选择 arr[start .. end] 中的一个元素作为一个基准元素,来对 arr[start .. end] 进行分区,然后重新排列 arr[start .. end],以便所有小于基准的条目都在基准的左侧,所有大于或等于基准的条目都在基准的右侧。
实际上,分区步骤重新排列了 arr[start..end],以使它由子列表 1、基准元素和子列表 2 组成,如图 1 所示。

图 1 快速排序以基准元素为中心进行分区
根据选定的基准元素的值,两个子列表中的一个或另一个可能是空的。例如,如果基准元素碰巧是最小数组元素,那么将不会有数组条目小于基准元素,所以子列表 1 将是空的。
请注意,一旦分区阶段完成,则会出现如图 1 所示的情况,基准元素将在正确的位置。通过递归地将快速排序过程应用于两个子列表,每个子列表将被分区,将任何被选择为该子列表的基准元素放置在正确的位置。这个过程一直持续到子列表的长度最多为 1 止。此时,原始数组将被排序。
假设有一个函数如下:
int partition(int arr[], int start, int end)
当它被调用时将执行以下操作:- 从 arr[start..end] 中选择一个基准元素。
- 重新排列 arr[Stot..end],使数组分区为子列表 1、基准元素和子列表 2(见图 1),这样基准元素在位置 p,而子列表 1 和子列表 2 则分别在 arr[start.. p-1] 和 arr[p+1 .. end]。
- 返回基准元素的位置 p。
然后即可在 C++ 中实现快速排序,如下所示:
void 快速排序(int arr[], int start, int end)
{
if (start < end)
{
//给数组分区并获得基准元素的位置
int p = partition(arr, start, end);
//排序小于基准元素的分区
快速排序(arr, start, p-1);
//排序大于基准元素的分区
快速排序(arr, p + 1, end);
}
}
现在来思考一下分割数组段 arr[start.. end] 的过程。分区算法选择 arr[start] 作为基准元素,然后分阶段在基准元素的左侧和右侧构建两个子列表。最初,已经分区的数组的部分只由它本身的基准元素组成。实际上,初始情况如图 1 所示,其中子列表 1 和子列表 2 是空的,并且所有尚未被添加到子列表 1 分区的数组条目均位于右边的子列表 2。分区的主要思想是按一次一个元素的方式扩展数组分区部分。设想元素 X 刚好位于子列表 2 最右侧,如果这个 X 大于或等于基准元素,则将其添加到子列表 2 的末尾(把它留在原来的位置即可),然后继续考虑下一个元素;如果 X 小于基准元素,则将其添加到子元素 1 的末尾,方法是将其放到基准元素的左侧。
要做到这一点,有一种方式是将 X 存储在临时位置,将子列表 2 中的每个元素向右移动一个位置,将基准元素也向右移动一个位置,然后将 X 放入由基准元素腾出来的数组位置。这种策略虽然简单,但是需要移动太多的数组元素,因此并不是有效的算法。
相反,我们可以更高效地将 X 放置在基准元素的左侧,方法是首先使用 X 与刚好在基准元素右侧的数组项 Y 交换,然后再让 X 与基准元素进行交换。第一次交换将 Y (大于或等于基准元素)置于子列表 2 的末尾,同时将 X 放置在与基准元素相邻的位置;第二次交换则把 X 放在基准元素的左侧。如此重复,直到整个列表已被分区。
执行分区操作的 partition 函数代码如下:
int partition(int arr[], int start, int end)
{
//釆用要分区的子范围中的第一个元素作为基准元素
int pivotValue = arr[start];
int pivotPosition = start;
//重新排列分区子范围中除基准元素之外的从start到end的兀素
for (int pos = start + 1; pos <= end; pos++)
{
if (arr[pos] < pivotValue)
{
// arr [scan]是“当前”项目 //使用这个当前项目和刚好位于基准元素右侧的元素交换
swap(arr[pivotPosition + 1], arr[pos]);
//使用当前项目和基准元素交换
swap(arr[pivotPosition], arr[pivotPosition + 1]);
//调整基准元素的位置使基准元素项目保持不变
pivotPosition ++;
}
}
return pivotPosition;
}
请注意,partition 中使用的 swap 函数是标准模板库的一部分,需要包含 <algorithm> 头文件才能使用它。 下面的程序演示了快速排序算法的实际应用:
// This program demonstrates the Quicksort algorithm. #include <iostream> #include <algorithm> //needed for swap function using namespace std; // Function prototypes void quicksort (int [], int, int); int partition (int [], int, int); int main() { //Array to be sorted const int SIZE = 10; int array[SIZE] = {17, 53, 9, 2, 30, 1, 82, 64, 26, 5}; // Echo the array to be sorted for (int k = 0; k < SIZE; k++) cout << array[k] << " "; cout << endl; // Sort the array using Quicksort quicksort (array, 0, SIZE-1); // Print the sorted array for (int k = 0; k < SIZE; k++) cout << array[k] << " "; cout << endl; return 0; } void quicksort (int arr[], int start, int end) { if (start < end) { // Partition the array and get the pivot point int p = partition(arr, start, end); // Sort the portion before the pivot point quicksort(arr, start, p - 1); // Sort the portion after the pivot point quicksort(arr, p + 1, end); } } int partition(int arr[], int start, int end) { // The pivot element is taken to be the element at // the start of the subrange to be partitioned int pivotValue = arr[start]; int pivotPosition = start; // Rearrange the rest of the array elements to partition the subrange from start to end for (int pos = start + 1; pos <= end; pos++) { if (arr[pos] < pivotValue) { // arr[scan] is the "current" item. // Swap the current item with the item to the // right of the pivot element swap(arr[pivotPosition + 1], arr[pos]); // Swap the current item with the pivot element swap(arr[pivotPosition], arr[pivotPosition + 1]); // Adjust the pivot position so it stays with the // pivot element pivotPosition ++; } } return pivotPosition; }程序运行结果为:
17 53 9 2 30 1 82 64 26 5
1 2 5 9 17 26 30 53 64 82
所有教程
- C语言入门
- C语言编译器
- C语言项目案例
- 数据结构
- C++
- STL
- C++11
- socket
- GCC
- GDB
- Makefile
- OpenCV
- Qt教程
- Unity 3D
- UE4
- 游戏引擎
- Python
- Python并发编程
- TensorFlow
- Django
- NumPy
- Linux
- Shell
- Java教程
- 设计模式
- Java Swing
- Servlet
- JSP教程
- Struts2
- Maven
- Spring
- Spring MVC
- Spring Boot
- Spring Cloud
- Hibernate
- Mybatis
- MySQL教程
- MySQL函数
- NoSQL
- Redis
- MongoDB
- HBase
- Go语言
- C#
- MATLAB
- JavaScript
- Bootstrap
- HTML
- CSS教程
- PHP
- 汇编语言
- TCP/IP
- vi命令
- Android教程
- 区块链
- Docker
- 大数据
- 云计算