什么是二叉树,二叉树及其应用
二叉树是一个结点的集合,其中每个结点最多与两个后继结点相关联,分别称为左侧子结点和右侧子结点。二叉树中的每个结点并不是全都有两个子结点,也可能只有一个结点或两个结点都可能被省略。在二叉树中,没有子结点的结点称为叶结点。
包含子结点的结点称为其子结点的父结点。对于一个定义为二叉树的非空的结点集合,每个结点必须至多有一个父结点,并且必须有一个结点是没有父结点的。这个没有父结点的结点称为二叉树的根结点。一个空的结点集合可以构成一个空的二叉树。
链表和二叉树有一些相似之处。二叉树的根对应于链表的头部,二叉树结点的子结点对应于链表中的后继结点,二叉树结点的父结点对应于链表中结点的前驱结点。当然,空链表的模拟是空的二叉树。
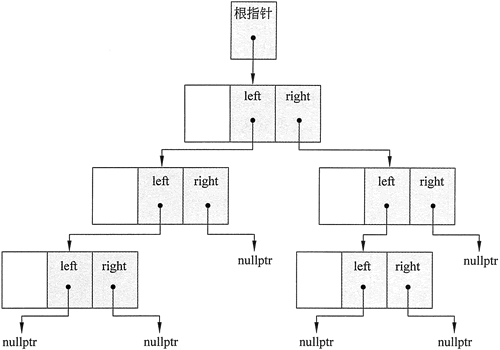
图 1 二叉树示意图
二叉树之所以称为树,是因为它们类似于倒置的树。任何非空树都可以分为根结点、左子树和右子树。直观地看,子树就是从一个特定的结点向下的树的整个分支。图 2 显示了如图 1 所示二叉树的左子树。
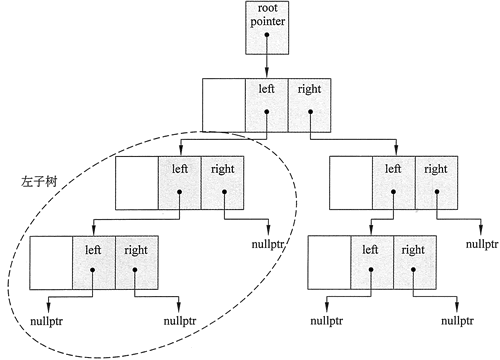
图 2 非空二叉树可以分为根结点、左子树和右子树
反观二叉树及其相似概念的结构则不同,它们是可用于大量信息搜索的优秀数据结构。它们常用于数据库应用程序,以组织键值,建立对数据库记录的索引。当用来方便搜索时,二叉树称为二叉搜索树。
信息存储在二叉搜索树中,将使树中的信息搜索变得简单。例如,来看图 3 中的二叉搜索树示例。
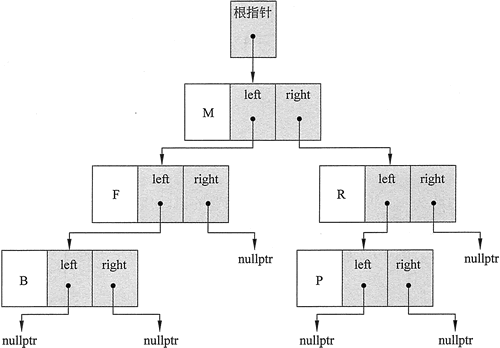
图 3 二叉搜索树示例
该图描绘了一个二叉搜索树,每个结点存储了一个字母,根结点保存的是字母 M。根结点的左侧子结点保存了字母 F,右侧子结点保存的是 R。
事实上,在二叉搜索树中,结点左侧的所有结点的值都小于结点的值。同样,结点右侧的所有结点的值都大于结点的数据。
当应用程序搜索二叉搜索树时,它将从根结点开始。如果根结点不包含搜索值,则根据搜索值是小于还是大于根结点的值,应用程序会相应分支到左侧或右侧子结点。这个过程一直持续到找到值或者确定搜索值不在树中。图 4 显示了在所显示的二叉树中查找字母 P 的搜索模式。
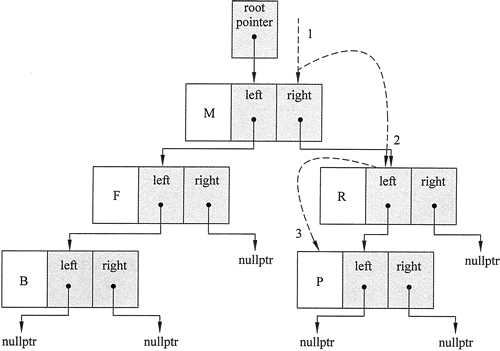
图 4 在二叉树中查找字母 P
这种搜索二叉树的方式让人想起在排序的数组上使用的二分搜索技术。假设二叉树是平衡的(意味着在每个结点处,左右子树的结点数大致相同),则搜索将在每一步中将剩余要搜索的树的大小减小一半,这使得在相对较少的步骤中搜索包含大量信息的树成为可能。
包含子结点的结点称为其子结点的父结点。对于一个定义为二叉树的非空的结点集合,每个结点必须至多有一个父结点,并且必须有一个结点是没有父结点的。这个没有父结点的结点称为二叉树的根结点。一个空的结点集合可以构成一个空的二叉树。
链表和二叉树有一些相似之处。二叉树的根对应于链表的头部,二叉树结点的子结点对应于链表中的后继结点,二叉树结点的父结点对应于链表中结点的前驱结点。当然,空链表的模拟是空的二叉树。
二叉树的实现
二叉树可用于将值存储到其结点中。因此,二叉树中的结点就是一个结构或类对象,它包含一个用于存储值的成员,以及另外两个指向该结点的左侧和右侧子结点的成员:
struct TreeNode
{
int value;
TreeNode *left;
TreeNode *right;
};
二叉树本身就是由指向根结点的指针所代表的。图 1 给出了一个二叉树示例,其中未显示结点中存储的值。如果该结点不具有相应的子结点,则结点中的 left 指针或 right 指针将设置为 nullptr。

图 1 二叉树示意图
二叉树之所以称为树,是因为它们类似于倒置的树。任何非空树都可以分为根结点、左子树和右子树。直观地看,子树就是从一个特定的结点向下的树的整个分支。图 2 显示了如图 1 所示二叉树的左子树。

图 2 非空二叉树可以分为根结点、左子树和右子树
二叉树的应用
对于任何线性数据结构(如数组或标准链表)来说,如果在其结构体中保存了大量信,那么在搜索其数据时速度会较慢,这是因为线性数据结构的连续性所致。反观二叉树及其相似概念的结构则不同,它们是可用于大量信息搜索的优秀数据结构。它们常用于数据库应用程序,以组织键值,建立对数据库记录的索引。当用来方便搜索时,二叉树称为二叉搜索树。
信息存储在二叉搜索树中,将使树中的信息搜索变得简单。例如,来看图 3 中的二叉搜索树示例。

图 3 二叉搜索树示例
该图描绘了一个二叉搜索树,每个结点存储了一个字母,根结点保存的是字母 M。根结点的左侧子结点保存了字母 F,右侧子结点保存的是 R。
事实上,在二叉搜索树中,结点左侧的所有结点的值都小于结点的值。同样,结点右侧的所有结点的值都大于结点的数据。
当应用程序搜索二叉搜索树时,它将从根结点开始。如果根结点不包含搜索值,则根据搜索值是小于还是大于根结点的值,应用程序会相应分支到左侧或右侧子结点。这个过程一直持续到找到值或者确定搜索值不在树中。图 4 显示了在所显示的二叉树中查找字母 P 的搜索模式。

图 4 在二叉树中查找字母 P
这种搜索二叉树的方式让人想起在排序的数组上使用的二分搜索技术。假设二叉树是平衡的(意味着在每个结点处,左右子树的结点数大致相同),则搜索将在每一步中将剩余要搜索的树的大小减小一半,这使得在相对较少的步骤中搜索包含大量信息的树成为可能。
所有教程
- C语言入门
- C语言编译器
- C语言项目案例
- 数据结构
- C++
- STL
- C++11
- socket
- GCC
- GDB
- Makefile
- OpenCV
- Qt教程
- Unity 3D
- UE4
- 游戏引擎
- Python
- Python并发编程
- TensorFlow
- Django
- NumPy
- Linux
- Shell
- Java教程
- 设计模式
- Java Swing
- Servlet
- JSP教程
- Struts2
- Maven
- Spring
- Spring MVC
- Spring Boot
- Spring Cloud
- Hibernate
- Mybatis
- MySQL教程
- MySQL函数
- NoSQL
- Redis
- MongoDB
- HBase
- Go语言
- C#
- MATLAB
- JavaScript
- Bootstrap
- HTML
- CSS教程
- PHP
- 汇编语言
- TCP/IP
- vi命令
- Android教程
- 区块链
- Docker
- 大数据
- 云计算