多路平衡归并排序(胜者树、败者树)算法详解
通过上一节对于外部排序的介绍得知:对于外部排序算法来说,其直接影响算法效率的因素为读写外存的次数,即次数越多,算法效率越低。若想提高算法的效率,即减少算法运行过程中读写外存的次数,可以增加 k –路平衡归并中的 k 值。
但是经过计算得知,如果毫无限度地增加 k 值,虽然会减少读写外存数据的次数,但会增加内部归并的时间,得不偿失。
例如在上节中,对于 10 个临时文件,当采用 2-路平衡归并时,若每次从 2 个文件中想得到一个最小值时只需比较 1 次;而采用 5-路平衡归并时,若每次从 5 个文件中想得到一个最小值就需要比较 4 次。以上仅仅是得到一个最小值记录,如要得到整个临时文件,其耗费的时间就会相差很大。
为了避免在增加 k 值的过程中影响内部归并的效率,在进行 k-路归并时可以使用“败者树”来实现,该方法在增加 k 值时不会影响其内部归并的效率。
在树形选择排序一节中,对于无序表
这棵树与败者树正好相反,是一棵“胜者树”。因为树中每个非终端结点(除叶子结点之外的其它结点)中的值都表示的是左右孩子相比较后的较小值(谁最小即为胜者)。例如叶子结点 49 和 38 相对比,由于 38 更小,所以其双亲结点中的值保留的是胜者 38。然后用 38 去继续同上层去比较,一直比较到树的根结点。
而败者树恰好相反,其双亲结点存储的是左右孩子比较之后的失败者,而胜利者则继续同其它的胜者去比较。
例如还是图 1 中,叶子结点 49 和 38 比较,38 更小,所以 38 是胜利者,49 为失败者,但由于是败者树,所以其双亲结点存储的应该是 49;同样,叶子结点 65 和 97 比较,其双亲结点中存储的是 97 ,而 65 则用来同 38 进行比较,65 会存储到 97 和 49 的双亲结点的位置,38 继续做后续的胜者比较,依次类推。
当最终胜者判断完成后,只需要更新叶子结点 b3 的值,即导入关键字 15,然后让该结点不断同其双亲结点所表示的关键字进行比较,败者留在双亲结点中,胜者继续向上比较。
例如,叶子结点 15 先同其双亲结点 ls[4] 中表示的 b4 中的 12 进行比较,12 为胜利者,则 ls[4] 改为 15,然后 12 继续同 ls[2] 中表示的 10 做比较,10 为胜者,然后 10 继续同其双亲结点 ls[1] 表示的 b1(关键字 9)作比较,最终 9 为胜者。整个过程如下图所示:
但是经过计算得知,如果毫无限度地增加 k 值,虽然会减少读写外存数据的次数,但会增加内部归并的时间,得不偿失。
例如在上节中,对于 10 个临时文件,当采用 2-路平衡归并时,若每次从 2 个文件中想得到一个最小值时只需比较 1 次;而采用 5-路平衡归并时,若每次从 5 个文件中想得到一个最小值就需要比较 4 次。以上仅仅是得到一个最小值记录,如要得到整个临时文件,其耗费的时间就会相差很大。
为了避免在增加 k 值的过程中影响内部归并的效率,在进行 k-路归并时可以使用“败者树”来实现,该方法在增加 k 值时不会影响其内部归并的效率。
败者树实现内部归并
败者树是树形选择排序的一种变形,本身是一棵完全二叉树。在树形选择排序一节中,对于无序表
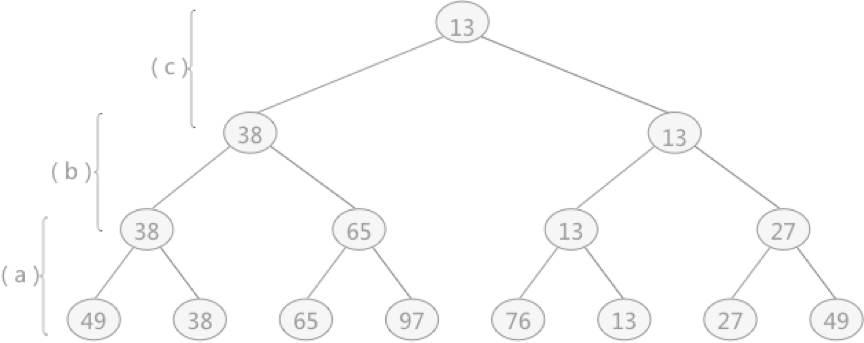
{49,38,65,97,76,13,27,49}创建的完全二叉树如图 1 所示,构建此树的目的是选出无序表中的最小值。这棵树与败者树正好相反,是一棵“胜者树”。因为树中每个非终端结点(除叶子结点之外的其它结点)中的值都表示的是左右孩子相比较后的较小值(谁最小即为胜者)。例如叶子结点 49 和 38 相对比,由于 38 更小,所以其双亲结点中的值保留的是胜者 38。然后用 38 去继续同上层去比较,一直比较到树的根结点。

图 1 胜者树
而败者树恰好相反,其双亲结点存储的是左右孩子比较之后的失败者,而胜利者则继续同其它的胜者去比较。
例如还是图 1 中,叶子结点 49 和 38 比较,38 更小,所以 38 是胜利者,49 为失败者,但由于是败者树,所以其双亲结点存储的应该是 49;同样,叶子结点 65 和 97 比较,其双亲结点中存储的是 97 ,而 65 则用来同 38 进行比较,65 会存储到 97 和 49 的双亲结点的位置,38 继续做后续的胜者比较,依次类推。
胜者树和败者树的区别就是:胜者树中的非终端结点中存储的是胜利的一方;而败者树中的非终端结点存储的是失败的一方。而在比较过程中,都是拿胜者去比较。

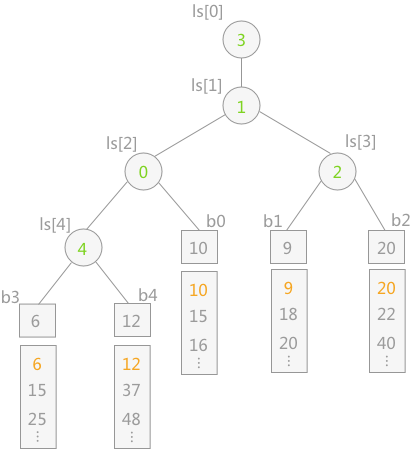
图 2 败者树
如图 2 所示为一棵 5-路归并的败者树,其中 b0—b4 为树的叶子结点,分别为 5 个归并段中存储的记录的关键字。 ls 为一维数组,表示的是非终端结点,其中存储的数值表示第几归并段(例如 b0 为第 0 个归并段)。ls[0] 中存储的为最终的胜者,表示当前第 3 归并段中的关键字最小。当最终胜者判断完成后,只需要更新叶子结点 b3 的值,即导入关键字 15,然后让该结点不断同其双亲结点所表示的关键字进行比较,败者留在双亲结点中,胜者继续向上比较。
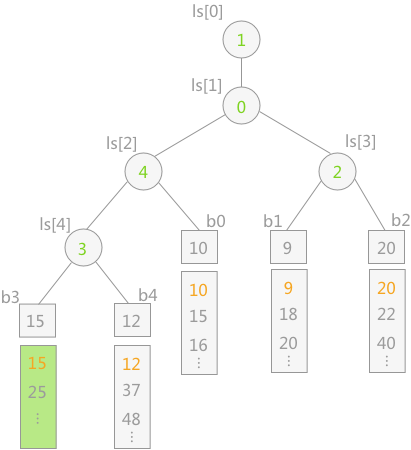
例如,叶子结点 15 先同其双亲结点 ls[4] 中表示的 b4 中的 12 进行比较,12 为胜利者,则 ls[4] 改为 15,然后 12 继续同 ls[2] 中表示的 10 做比较,10 为胜者,然后 10 继续同其双亲结点 ls[1] 表示的 b1(关键字 9)作比较,最终 9 为胜者。整个过程如下图所示:

注意:为了防止在归并过程中某个归并段变为空,处理的办法为:可以在每个归并段最后附加一个关键字为最大值的记录。这样当某一时刻选出的冠军为最大值时,表明 5 个归并段已全部归并完成。(因为只要还有记录,最终的胜者就不可能是附加的最大值)
败者树内部归并的具体实现
#include <stdio.h>
#define k 5
#define MAXKEY 10000
#define MINKEY -1
typedef int LoserTree[k];//表示非终端结点,由于是完全二叉树,所以可以使用一维数组来表示
typedef struct {
int key;
}ExNode,External[k+1];
External b;//表示败者树的叶子结点
//a0-a4为5个初始归并段
int a0[]={10,15,16};
int a1[]={9,18,20};
int a2[]={20,22,40};
int a3[]={6,15,25};
int a4[]={12,37,48};
//t0-t4用于模拟从初始归并段中读入记录时使用
int t0=0,t1=0,t2=0,t3=0,t4=0;
//沿从叶子结点b[s]到根结点ls[0]的路径调整败者树
void Adjust(LoserTree ls,int s){
int t=(s+k)/2;
while (t>0) {
//判断每一个叶子结点同其双亲结点中记录的败者的值相比较,调整败者的值,其中 s 一直表示的都是胜者
if (b[s].key>b[ls[t]].key) {
int swap=s;
s=ls[t];
ls[t]=swap;
}
t=t/2;
}
//最终将胜者的值赋给 ls[0]
ls[0]=s;
}
//创建败者树
void CreateLoserTree(LoserTree ls){
b[k].key=MINKEY;
//设置ls数组中败者的初始值
for (int i=0; i<k; i++) {
ls[i]=k;
}
//对于每一个叶子结点,调整败者树中非终端结点中记录败者的值
for (int i=k-1; i>=0; i--) {
Adjust(ls, i);
}
}
//模拟从外存向内存读入初始归并段中的每一小部分
void input(int i){
switch (i) {
case 0:
if (t0<3) {
b[i].key=a0[t0];
t0++;
}else{
b[i].key=MAXKEY;
}
break;
case 1:
if (t1<3) {
b[i].key=a1[t1];
t1++;
}else{
b[i].key=MAXKEY;
}
break;
case 2:
if (t2<3) {
b[i].key=a2[t2];
t2++;
}else{
b[i].key=MAXKEY;
}
break;
case 3:
if (t3<3) {
b[i].key=a3[t3];
t3++;
}else{
b[i].key=MAXKEY;
}
break;
case 4:
if (t4<3) {
b[i].key=a4[t4];
t4++;
}else{
b[i].key=MAXKEY;
}
break;
default:
break;
}
}
//败者树的建立及内部归并
void K_Merge(LoserTree ls){
//模拟从外存中的5个初始归并段中向内存调取数据
for (int i=0; i<=k; i++) {
input(i);
}
//创建败者树
CreateLoserTree(ls);
//最终的胜者存储在 is[0]中,当其值为 MAXKEY时,证明5个临时文件归并结束
while (b[ls[0]].key!=MAXKEY) {
//输出过程模拟向外存写的操作
printf("%d ",b[ls[0]].key);
//继续读入后续的记录
input(ls[0]);
//根据新读入的记录的关键字的值,重新调整败者树,找出最终的胜者
Adjust(ls,ls[0]);
}
}
int main(int argc, const char * argv[]) {
LoserTree ls;
K_Merge(ls);
return 0;
}
运行结果:
6 9 10 12 15 15 16 18 20 20 22 25 37 40 48
总结
本节介绍了通过使用败者树来实现增加 k-路归并的规模来提高外部排序的整体效率。但是对于 k 值得选择也并不是一味地越大越好,而是需要综合考虑选择一个合适的 k 值。所有教程
- C语言入门
- C语言编译器
- C语言项目案例
- 数据结构
- C++
- STL
- C++11
- socket
- GCC
- GDB
- Makefile
- OpenCV
- Qt教程
- Unity 3D
- UE4
- 游戏引擎
- Python
- Python并发编程
- TensorFlow
- Django
- NumPy
- Linux
- Shell
- Java教程
- 设计模式
- Java Swing
- Servlet
- JSP教程
- Struts2
- Maven
- Spring
- Spring MVC
- Spring Boot
- Spring Cloud
- Hibernate
- Mybatis
- MySQL教程
- MySQL函数
- NoSQL
- Redis
- MongoDB
- HBase
- Go语言
- C#
- MATLAB
- JavaScript
- Bootstrap
- HTML
- CSS教程
- PHP
- 汇编语言
- TCP/IP
- vi命令
- Android教程
- 区块链
- Docker
- 大数据
- 云计算