二叉搜索树基本操作详解
本节将介绍可能在二叉搜索树上执行的一些基本操作。接下来要讲解的是一个简单的类,该类实现了用一个二叉树来存储整数值。
IntBinaryTree 的公共成员函数包括:构造函数、析构函数、用于在树中插入新数字的成员函数、用于搜索树以确定给定的数字是否在树中的成员函数、用于从树中移除数字的成员函数,以及根据不同的顺序显示存储在树中的数字的成员函数。
下面的程序演示了创建一个 IntBinaryTree 对象和使用公共 insert 成员函数来构建一个二叉搜索树:
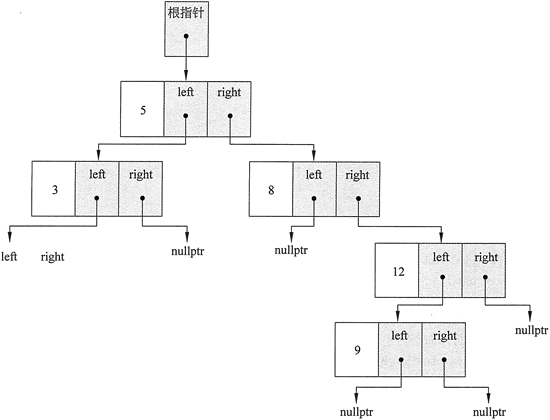
图 1 使用 insert 成员函数构建的二叉树
例如,如果根结点由一个指针表示:
注意,如图 1 所示的树的形状由值的插入顺序决定。根结点保存值 5,因为它是插入的第一个值。通过遍历该函数,可以看到其他结点是如何出现在它们图示的位置上的。
中序遍历算法的实现思路是:
前序遍历算法的实现思路是:
后序遍历算法的实现思路是:
IntBinaryTree 类可以使用这 3 种算法显示树中的所有值。该算法将由以下内联公共成员函数进行初始化:
该函数只是开始搜索整个树。将 num (正在搜索的值)与当前正在搜索的树的根值进行比较。如果值匹配,则函数返回 true。如果该值不匹配,则该函数用其左子树或其右子树替换该树,并继续搜索。当函数找到值或搜索树变空时,搜索将终止。
删除结点 X 的过程取决于其子结点的数量。如果 X 没有子元素,则首先找到它的父元素,将连接到 X 的父元素的子指针设置为 nullptr,然后释放分配给 X 的内存。如果 X 是树的根,则刚刚描述的过程不会工作。在这种情况下,只需删除 X,并将指向树根的指针设置为 nullptr。
删除非叶结点的过程必须确保该结点链接的子树保持为树的一部分。该过程将根据被删除的结点是否有一个或两个子结点而有所不同。图 2 显示了一个树,其中有一个要删除的结点,而该结点本身具有一个子树。
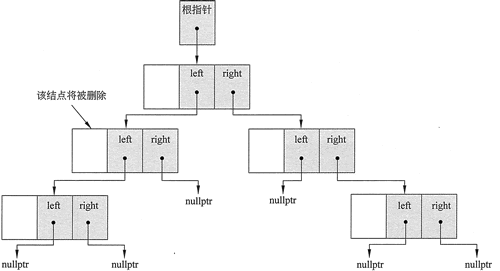
图 2 要删除的结点具有一个子树
图 3 显示了如何将结点的子树与其父结点链接起来。
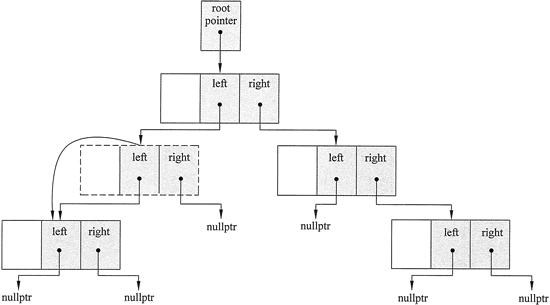
图 3 将结点的子树与其父结点链接起来以方便删除结点
但是,当要删除的结点有 2 个子树时,这个问题就变得不那么容易被解决,如图 4 所示。
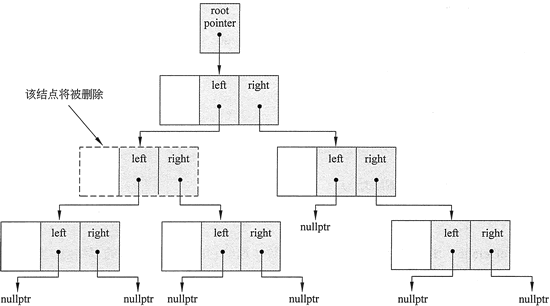
图 4 如果要删除的结点有 2 个子树则问题就变得相对复杂
很显然,不能将结点的两个子树都连接到它的父结点(因为任何二叉树的结点都不能拥有 3 个子结点),所以必须有另一种解决方案。解决这个问题的一种方法是将结点的右侧子树连接到父结点,然后在右侧子树中找到一个位置来连接左侧子树。结果如图 5 所示。
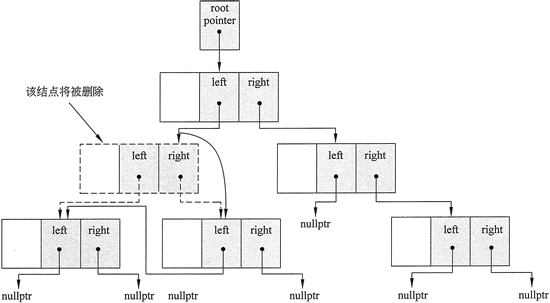
图 5 删除拥有 2 个子结点的结点的解决方案
请注意,在将左侧子树连接到右侧子树时,必须注意保留二叉树的搜索属性。
从 IntBinaryTree 对象中删除值是通过调用公共成员函数 remove 来完成的,后者又调用同名的私有成员函数。后面这个函数被传递(二叉搜索树的根)tree 和一个要从树中删除的值 num:
以下是 remove 函数的代码:
现在来看一看 makeDeletion 函数背后的逻辑,它有以下几种情况需要考虑:
以下是整个函数的代码:
创建二叉搜索树
现在使用 IntBinaryTree 类来演示基本的二叉树操作。在本示例中,二叉树结点的基础是下面的类声明:
class TreeNode
{
int value;
TreeNode *left;
TreeNode *right;
TreeNode(int value1,TreeNode *left1 = nullptr,TreeNode *right1 = nullptr)
{
value = value1;
left = left1;
right = right1;
}
};
请注意,树的每个结点都有一个 value 成员,另外还有两个指针,用于跟踪结点的左侧和右侧子结点。这个类只能被 IntBinaryTree 的方法使用。
//IntBinaryTree.h的内容
class IntBinaryTree
{
private:
//The TreeNode struct is used to build the tree.
struct TreeNode
{
int value;
TreeNode *left;
TreeNode *right;
TreeNode(int value1,TreeNode *left1 = nullptr,TreeNode *right1 = nullptr)
{
value = value1;
left = left1;
right = right1;
}
};
TreeNode *root; // Pointer to the root of the tree
// Various helper member functions.
void insert(TreeNode *&, int);
void destroySubtree(TreeNode *);
void remove(TreeNode *&, int);
void makeDeletion(TreeNode *&);
void displayInOrder(TreeNode *) const;
void displayPreOrder(TreeNode *) const;
void displayPostOrder(TreeNode *) const;
public:
// These member functions are the public interface.
IntBinaryTree。 // Constructor
{
root = nullptr;
}
~IntBinaryTree() // Destructor
{
destroySubtree(root);
}
void insert(int num)
{
insert (root, num);
}
bool search(int) const;
void remove(int num)
{
remove(root, num);
}
void showInOrder(void) const
{
displayInOrder(root);
}
void showPreOrder() const
{
displayPreOrder(root);
}
void showPostOrder() const
{
displayPostOrder(root);
}
}
除了 TreeNode 类声明之外,该类还有一个 root 成员。这是一个指向二叉树根结点的指针,起着类似于链表中 head 指针的作用。在许多情况下,将指向二叉树根结点的指针视为二叉树本身是很有用的。因此,可以写作如下形式:
TreeNode *tree;
或
TreeNode *root;
IntBinaryTree Tree;
为了避免混淆,当使用由 IntBinaryTree 类的对象表示二叉树时,该二叉树的标识符首字母釆用大写形式,例如 "IntBinaryTreeTree;";当使用由指向其根结点的指针表示二叉树时,则该二叉树的标识符首字母釆用小写形式,例如 "TreeNode *root;"。IntBinaryTree 的公共成员函数包括:构造函数、析构函数、用于在树中插入新数字的成员函数、用于搜索树以确定给定的数字是否在树中的成员函数、用于从树中移除数字的成员函数,以及根据不同的顺序显示存储在树中的数字的成员函数。
下面的程序演示了创建一个 IntBinaryTree 对象和使用公共 insert 成员函数来构建一个二叉搜索树:
// This program builds a binary tree with 5 nodes. #include <iostream> #include "IntBinaryTree.h" using namespace std; int main() { IntBinaryTree tree; cout << "Inserting numbers. "; tree.insert (5); tree.insert(8); tree.insert (3); tree.insert(12); tree.insert (9); cout << "Done. \n"; return 0; }程序执行结果如图 1 所示:

图 1 使用 insert 成员函数构建的二叉树
二叉搜索树操作的实现
许多二叉树操作都有非常自然的递归实现。这是因为二叉树是一种固有的递归数据结构:每一个非空二叉树都由一个根结点和左右子树组成,当然,这些子树也都是二叉树。许多二叉树操作可以通过在根结点处执行一些处理然后在左右子树上递归地执行操作来实现。例如,如果根结点由一个指针表示:
TreeNode *tree;
那么根结点中的值将是 tree->value,左右子树将由 tree->left 和 tree->right 给出。递归操作可能首先处理 tree->value,然后递归操作 tree->left 和 tree->right。二叉搜索树插入元素
将数字插入到二叉搜索树中的工作由私有成员函数执行,即:insert(TreeNode *&tree, int num)
该语句将指针 tree 传递给二叉搜索树的根结点,并将数字 num 插入树中。它使用递归策略:如果二叉树是空的(这是递归的基本情况),那么它将创建一个新的 TreeNode 对象,其值成员是给定的数字,并使其成为树的根:
if (!tree)
{
tree = new TreeNode(num);
return;
}
但是,如果二叉搜索树不为空,则 insert 函数会将 num 与 tree->value(根结点中的值)进行比较。根据这个比较的结果,新值被递归地插入到左边或右边的子树中:
if (num < tree->value)
insert(tree->left, num);
else
insert(tree->right, num);
整个函数给定如下:
void IntBinaryTree::insert(TreeNode * &tree, int num)
{
//如果树是空的,则创建一个新结点
//并且使该结点成为根结点
if (!tree)
{
tree = new TreeNode(num);
return;
}
//如果num已经在树中,则返回
if (tree->value == num)
return;
//如果树不为空,则插入新结点到左子树或右子树中
if (num < tree->value)
insert(tree->left, num);
else
insert(tree->right, num);
}
请注意,该函数被传递对指针的引用,因为传递的指针可能需要由函数修改。这也是 remove 和 makeDeletion 函数通过引用传递其形参的原因。注意,如图 1 所示的树的形状由值的插入顺序决定。根结点保存值 5,因为它是插入的第一个值。通过遍历该函数,可以看到其他结点是如何出现在它们图示的位置上的。
二叉搜索树的遍历
遍历非空二叉树和处理每个结点的值有3种常用的方法:中序遍历、前序遍历和后序遍历。这些方法中的每一个的最佳实现方式都是递归函数。中序遍历算法的实现思路是:
- 遍历结点的左子树。
- 结点的数据被处理。
- 遍历结点的右子树。
前序遍历算法的实现思路是:
- 结点的数据被处理。
- 遍历结点的左子树。
- 遍历结点的右子树。
后序遍历算法的实现思路是:
- 遍历结点的左子树。
- 遍历结点的右子树。
- 结点的数据被处理。
IntBinaryTree 类可以使用这 3 种算法显示树中的所有值。该算法将由以下内联公共成员函数进行初始化:
void showInOrder(void){ displayInOrder (root); }
void showPreOrder(){ displayPreOrder(root); }
void showPostOrder(){ displayPostOrder(root); }
void IntBinaryTree::displayInOrder(TreeNode *tree) const
{
if (tree)
{
displayInOrder(tree->left);
cout << tree->value << " ";
displayInOrder(tree->right);
}
}
void IntBinaryTree::displayPreOrder(TreeNode *tree) const
{
if (tree)
{
cout << tree->value << " ";
displayPreOrder(tree->left);
displayPreOrder(tree->right);
}
}
void IntBinaryTree::displayPostOrder(TreeNode *tree) const
{
if (tree)
{
displayPostOrder(tree->left);
displayPostOrder(tree->right);
cout << tree->value << " ";
}
}
下面的程序演示了这 3 种遍历方法中的每一种。
//This program builds a binary tree with 5 nodes. The nodes are displayed with inorderA preorder, and postorder algorithms.
#include <iostream>
#include "IntBinaryTree.h"
using namespace std;
int main()
{
IntBinaryTree tree;
cout << "Inserting the numbers 5 8 3 12 9.\n";
tree.insert(5);
tree.insert(8);
tree.insert(3);
tree.insert(12);
tree.insert(9);
cout << "Inorder traversal: ";
tree.showInOrder();
cout << "\nPreorder traversal: ";
tree.showPreOrder();
cout << "\nPostorder traversal: ";
tree.showPostOrder();
return 0;
}
程序执行结果:
Inserting the numbers 5 83 12 9.
Inorder traversal: 3 5 8 9 12
Preorder traversal: 5 3 8 12 9
Postorder traversal: 3 9 12 8 5
搜索二叉搜索树
IntBinarySearchTree 类具有公共成员函数 search,如果在树中找到给定值,则返回 true,否则返回 false。该函数只是开始搜索整个树。将 num (正在搜索的值)与当前正在搜索的树的根值进行比较。如果值匹配,则函数返回 true。如果该值不匹配,则该函数用其左子树或其右子树替换该树,并继续搜索。当函数找到值或搜索树变空时,搜索将终止。
bool IntBinaryTree::search(int num) const
{
TreeNode *tree = root;
while (tree)
{
if (tree->value == num)
return true;
else if (num < tree->value)
tree = tree->left;
else
tree = tree->right;
}
return false;
}
下面的程序演示了该函数:
//This program builds a binary tree with 5 nodes. The search function determines if the value 3 is in the tree.
#include <iostream>
#include "IntBinarytree.h"
using namespace std;
int main()
{
IntBinaryTree tree;
cout << "Inserting the numbers 5 8 3 12 9.\n";
tree.insert (5);
tree.insert(8);
tree.insert (3);
tree.insert (12);
tree.insert (9);
if (tree.search(3))
cout << "3 is found in the tree.\n";
else
cout << "3 was not found in the tree.\n";
return 0;
}
程序输出结果:
Inserting the numbers 5 83 12 9.
3 is found in the tree.
二叉搜索树删除元素
要移除一个元素,首先需要找到包含该元素的结点,然后才能删除该结点。删除结点 X 的过程取决于其子结点的数量。如果 X 没有子元素,则首先找到它的父元素,将连接到 X 的父元素的子指针设置为 nullptr,然后释放分配给 X 的内存。如果 X 是树的根,则刚刚描述的过程不会工作。在这种情况下,只需删除 X,并将指向树根的指针设置为 nullptr。
删除非叶结点的过程必须确保该结点链接的子树保持为树的一部分。该过程将根据被删除的结点是否有一个或两个子结点而有所不同。图 2 显示了一个树,其中有一个要删除的结点,而该结点本身具有一个子树。

图 2 要删除的结点具有一个子树
图 3 显示了如何将结点的子树与其父结点链接起来。

图 3 将结点的子树与其父结点链接起来以方便删除结点
但是,当要删除的结点有 2 个子树时,这个问题就变得不那么容易被解决,如图 4 所示。

图 4 如果要删除的结点有 2 个子树则问题就变得相对复杂
很显然,不能将结点的两个子树都连接到它的父结点(因为任何二叉树的结点都不能拥有 3 个子结点),所以必须有另一种解决方案。解决这个问题的一种方法是将结点的右侧子树连接到父结点,然后在右侧子树中找到一个位置来连接左侧子树。结果如图 5 所示。

图 5 删除拥有 2 个子结点的结点的解决方案
请注意,在将左侧子树连接到右侧子树时,必须注意保留二叉树的搜索属性。
从 IntBinaryTree 对象中删除值是通过调用公共成员函数 remove 来完成的,后者又调用同名的私有成员函数。后面这个函数被传递(二叉搜索树的根)tree 和一个要从树中删除的值 num:
remove (TreeNode *&tree, int num)
该函数使用了递归策略:- 如果树为空,则立即返回;
- 如果 num 小于存储在根结点中的值,则函数递归地从左子树中删除 num;
- 如果 num 大于存储在根结点中的值,则函数递归地从右子树中删除 num;
- 如果在根结点中找到 num,则将由 makeDeletion 函数来处理;
以下是 remove 函数的代码:
void IntBinaryTree::remove(TreeNode *&tree, int num)
{
if (tree == nullptr)
return;
if (num < tree->value)
remove(tree->left, num);
else if (num > tree->value)
remove(tree->right,num);
else
//已经找到要删除的结点
makeDeletion(tree);
}
makeDeletion 函数设计用来删除作为参数传递给它的二叉搜索树的根结点,留下由剩余结点组成的二叉搜索树。现在来看一看 makeDeletion 函数背后的逻辑,它有以下几种情况需要考虑:
- 传递给 makeDeletion 函数的树的根结点没有子结点。在这种情况下,删除根结点并用 nullptr 替换树。
- 树的根结点只有一个子结点。在这种情况下,可以删除根结点,并使用已被删除的根结点的子结点来代替树:
TreeNode *nodeToDelete = tree;
if (tree->right == nullptr)
tree = tree->left;
else if (tree->left == nullptr)
tree = tree->right;
- 传递给 makeDelete 的树有两个子结点。在这种情况下,删除根结点会留下两个子树,因此这两个子结点都需要进行一些处理。这里采用的策略是将两个子树合并为一个二叉搜索树,然后用合并的子树构建的树代替原树。如图 5 所示,可以将原始树的左子树连接作为原始树的右子树中最小结点的左子树。
以下是整个函数的代码:
void IntBinaryTree::makeDeletion(TreeNode *&tree)
{
//用于保存将被删除的结点
TreeNode *nodeToDelete = tree;
//用于找到左子树要连接的点
TreeNode *attachPoint;
if (tree->right == nullptr)
{
//使用其左子树替换该树
tree = tree->left;
}
else if (tree->left == nullptr)
{
//使用其右子树替换该树
tree = tree->right;
}
else//该结点有2个子结点
{
//移动到右子树
attachPoint = tree->right;
//找到右子树中的最小结点移动到最左侧
while (attachPoint->left != nullptr)
attachPoint = attachPoint->left;
//连接原始树的左子树作为右子树中的最小结点的左子树
attachPoint一>left = tree->left;
//使用右子树替换原始树
tree = tree->right;
}
//删除原始树
delete nodeToDelete;
}
下面的程序演示了这些函数:
// This program builds a binary tree with 5 nodes.
// The deleteNode function is used to remove 2 of them.
#include <iostream>
#include "IntBinaryTree.h"
using namespace std;
int main()
{
IntBinaryTree tree;
cout << "Inserting the numbers 5 8 3 12 9.";
tree.insert(5);
tree.insert(8);
tree.insert(3);
tree.insert(12);
tree.insert(9);
cout << "\nHere are the values in the tree:\n"; tree.showInOrder();
cout << "\nDeleting 8...\n";
tree.remove(8);
cout << "Deleting 12... \n";
tree.remove(12);
cout << "Now, here are the nodes:\n";
tree.showInOrder();
return 0;
}
程序输出结果:
Inserting the numbers 5 8 3 12 9.
Here are the values in the tree:
3 5 8 9 12
Deleting 8...
Deleting 12...
Now, here are the nodes: 3 5 9
所有教程
- C语言入门
- C语言编译器
- C语言项目案例
- 数据结构
- C++
- STL
- C++11
- socket
- GCC
- GDB
- Makefile
- OpenCV
- Qt教程
- Unity 3D
- UE4
- 游戏引擎
- Python
- Python并发编程
- TensorFlow
- Django
- NumPy
- Linux
- Shell
- Java教程
- 设计模式
- Java Swing
- Servlet
- JSP教程
- Struts2
- Maven
- Spring
- Spring MVC
- Spring Boot
- Spring Cloud
- Hibernate
- Mybatis
- MySQL教程
- MySQL函数
- NoSQL
- Redis
- MongoDB
- HBase
- Go语言
- C#
- MATLAB
- JavaScript
- Bootstrap
- HTML
- CSS教程
- PHP
- 汇编语言
- TCP/IP
- vi命令
- Android教程
- 区块链
- Docker
- 大数据
- 云计算