决策树和朴素贝叶斯算法简介
决策树算法
决策树(Decision Tree,DT)分类法是一个简单且广泛使用的分类技术。决策树是一个树状预测模型,它是由结点和有向边组成的层次结构。树中包含3种结点:根结点、内部结点和叶子结点。决策树只有一个根结点,是全体训练数据的集合。
树中的一个内部结点表示一个特征属性上的测试,对应的分支表示这个特征属性在某个值域上的输出。一个叶子结点存放一个类别,也就是说,带有分类标签的数据集合即为实例所属的分类。
1. 决策树案例
使用决策树进行决策的过程就是,从根结点开始,测试待分类项中相应的特征属性,并按照其值选择输出分支,直到到达叶子结点,将叶子结点存放的类别作为决策结果。图 1 是一个预测一个人是否会购买电脑的决策树。利用这棵树,可以对新记录进行分类。从根结点(年龄)开始,如果某个人的年龄为中年,就直接判断这个人会买电脑,如果是青少年,则需要进一步判断是否是学生,如果是老年,则需要进一步判断其信用等级。
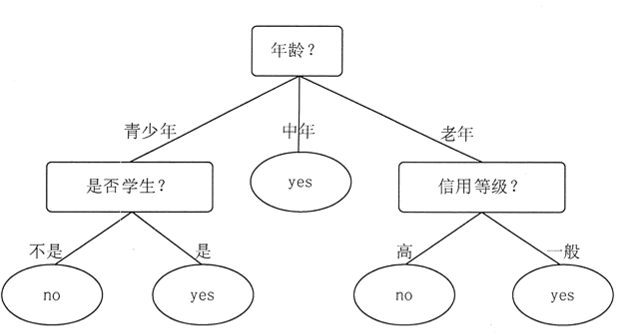
图 1 预测是否购买电脑的决策树
假设客户甲具备以下 4 个属性:年龄 20、低收入、是学生、信用一般。通过决策树的根结点判断年龄,判断结果为客户甲是青少年,符合左边分支,再判断客户甲是否是学生,判断结果为用户甲是学生,符合右边分支,最终用户甲落在“yes”的叶子结点上。所以预测客户甲会购买电脑。
2. 决策树的建立
决策树算法有很多,如 ID3、C4.5、CART 等。这些算法均采用自上而下的贪婪算法建立决策树,每个内部结点都选择分类效果最好的属性来分裂结点,可以分成两个或者更多的子结点,继续此过程直到这棵决策树能够将全部的训练数据准确地进行分类,或所有属性都被用到为止。1)特征选择
按照贪婪算法建立决策树时,首先需要进行特征选择,也就是使用哪个属性作为判断结点。选择一个合适的特征作为判断结点,可以加快分类的速度,减少决策树的深度。
特征选择的目标就是使得分类后的数据集比较纯。如何衡量一个数据集的纯度?这里就需要引入数据纯度概念——信息增益。
信息是个很抽象的概念。人们常常说信息很多,或者信息较少,但却很难说清楚信息到底有多少。
1948 年,信息论之父 Shannon 提出了“信息熵”的概念,才解决了对信息的量化度量问题。通俗来讲,可以把信息熵理解成某种特定信息的出现概率。信息嫡表示的是信息的不确定度,当各种特定信息出现的概率均匀分布时,不确定度最大,此时嫡就最大。反之,当其中的某个特定信息出现的概率远远大于其他特定信息的时候,不确定度最小,此时熵就很小。
所以,在建立决策树的时候,希望选择的特征能够使分类后的数据集的信息熵尽可能变小,也就是不确定性尽量变小。当选择某个特征对数据集进行分类时,分类后的数据集的信息嫡会比分类前的小,其差值表示为信息增益。信息增益可以衡量某个特征对分类结果的影响大小。
ID3 算法使用信息增益作为属性选择度量方法,也就是说,针对每个可以用来作为树结点的特征,计算如果采用该特征作为树结点的信息增益。然后选择信息增益最大的那个特征作为下一个树结点。
2)剪枝
在分类模型建立的过程中,很容易出现过拟合的现象。过拟合是指在模型学习训练中,训练样本达到非常高的逼近精度,但对检验样本的逼近误差随着训练次数呈现出先下降后上升的现象。过拟合时训练误差很小,但是检验误差很大,不利于实际应用。
决策树的过拟合现象可以通过剪枝进行一定的修复。剪枝分为预先剪枝和后剪枝两种。
预先剪枝是指,在决策树生长过程中,使用一定条件加以限制,使得在产生完全拟合的决策树之前就停止生长。
预先剪枝的判断方法也有很多,例如,信息增益小于一定阈值的时候通过剪枝使决策树停止生长。但如何确定一个合适的阈值也需要一定的依据,阈值太高会导致模型拟合不足,阈值太低又导致模型过拟合。
后剪枝是指,在决策树生长完成之后,按照自底向上的方式修剪决策树。后剪枝有两种方式,一种是用新的叶子结点替换子树,该结点的预测类由子树数据集中的多数类决定,另一种是用子树中最常使用的分支代替子树。
预先剪枝可能会过早地终止决策树的生长,而后剪枝一般能够产生更好的效果。但后剪枝在子树被剪掉后,决策树生长过程中的一部分计算就被浪费了。
3. Spark MLlib 决策树算法
Spark MLlib 支持连续型和离散型的特征变量,也就是既支持预测也支持分类。在 Spark MLlib 中、建立决策树时是按照信息增益选择划分特征的,它采用前向剪枝的方法来防止过拟合,当任意一个以下情况发生时,Spark MLlib 的决策树结点就终止划分,形成叶子结点。
- 树高度达到指定的最大高度 maxDepth。
- 当前结点的所有属性分裂带来的信息増益都小于指定的阈值 minInstancesPerNode。
- 结点分割出的子结点的最少样本数量小于阈值 minInstancesPerNode。
Spark MLlib 的决策树算法是由 DecisionTree 类实现的,该类支持二元或多标签分类,并且还支持预测。用户通过配置参数 Strategy 来说明是进行分类,还是进行预测,以及使用什么方法进行分类。
1)Spark MLlib 的 DecisionTree 的训练函数
DecisionTree 调用 trainClassifier 方法进行分类训练,参数如下所示。
def trainClassifier(
input: RDD[LabeledPoint],
numClasses: Int,
categoricalFeaturesInfo: Map[Int,Int], impurity: String,
maxDepth:Int,
maxBins:Int): DecisionTreeModel
| 名称 | 说明 |
|---|---|
| Input | 表示输入数据集,每个 RDD 元素代表一个数据点,每个数据点都包含标签和数据特征,对分类来讲,标签的值是 {0,1,...,numClasses-1}。 |
| numClasses | 表示分类的数量,默认值是 2。 |
| categoricalFeaturesInfo | 存储离散性属性的映射关系,例如,(5→4)表示数据点的第 5 个特征是离散性属性,有 4 个类别,取值为{0,1,2,3}。 |
| impurity | 表示信息纯度的计算方法,包括 Gini 参数或信息熵。 |
| maxDepth | 表示树的最大深度。 |
| maxBins | 表示每个结点的分支的最大值。 |
2)Spark MLlib 的 DecisionTree 的预测函数
DecisionTreeModel.predict 方法可以接收不同格式的数据输入参数,包括向量、RDD,返回的是计算出来的预测值。该方法的 API 如下。
def predict(features:Vector):Double
def predict(features: RDD[Vector]): RDD[Double]
4. Spark MLlib 决策树算法实例
实例:导入训练数据集,使用 ID3 决策树建立分类模型,采用信息增益作为选择分裂特征的纯度参数,最后使用构造好的决策树,对两个数据样本进行分类预测。该实例使用的数据存放在 dt.data 文档中,提供了 6 个点的特征数据和与其对应的标签,数据如下所示。
1 1:1 2:0 3:0 4:1
0 1:1 2:0 3:1 4:1
0 1:0 2:1 3:0 4:0
1 1:1 2:1 3:0 4:0
1 1:1 2:0 3:0 4:0
1 1:1 2:1 3:0 4:0
实现的代码如下所示。
import org.apache.spark.mllib.tree.DecisionTree
import org.apache.spark.mllib.util.MLUtils
import org.apache.spark.{SparkConf, SparkContext}
object DecisionTreeByEntropy {
def main(args: Array[String]) {
val conf = new SparkConf().setMaster("local[4]").setAppName ( "DecisionTreeByEntropy")
val sc = new SparkContext (conf)
//上载和分解数据
val data = MLUtils.loadLibSVMFile (sc, ("/home/hadoop/exercise/dt.data"))
val numClasses = 2 //设定分类数量
val categoricalFeaturesInfo = Map[Int,Int]() //设定输入格式
val impurity = "entropy" //设定信息增益的计算方式 val maxDepth = 5 //设定树的最大高度
val maxBins = 3 //设定分裂数据集如最大个数
//建立模型并打印结果
val model = DecisionTree.trainClassifier(data,numClasses,categoricalFeaturesInfo,impurity,maxDepth,maxBins)
printIn ("model.depth:"+ model.depth)
printIn ("model.numNodes:" + model.numNodes) printIn ("model.topNode:" + model.topNode)
//从数据集中抽取两个数据样本进行预测并打印结果
val labelAndPreds = data.take(2).map { point =>
val prediction = model.predict(point.features)
(point.label, prediction)
}
labelAndPreds.foreach(printIn)
sc.stop
}
}
运行以上代码将输出构建的决策分类树的信息,包括树的高度、结点数和树的根结点的详细信息,以及两个样本的实际值和预测值。具体信息如下。
model.depth:2
model.numNodes:5
model.topNode:id = 1, isLeaf = false, predict = 1.0 (prob = 0.6666666666666666),
impurity = 0.9182958340544896, split = Some(Feature = 0, threshold = 0.0, featureType = Continuous, categories = List())r
stats = Some(gain = 0.31668908831502096, impurity = 0.9182958340544896,
left impurity = 0.0, right impurity = 0.7219280948873623)
(1.0,1.0)
(0.0,0.0)
5. 算法优缺点
决策树是非常流行的分类算法。一般情况下,不需要任何领域知识或参数设置,它就可以处理高维数据。它对知识的表示是直观的,并且具有描述性,非常容易理解,有助于人工分析。用决策树进行学习和分类的步骤非常简单,效率高。决策树只需要一次构建,就可以反复使用,但每一次预测的最大计算次数不能超过决策树的深度。一般来讲,决策树具有较好的分类准确率,但是决策树的成功应用可能依赖于所拥有的建模数据。
朴素贝叶斯算法
朴素贝叶斯(Nawe Bayes)算法是一种十分简单的分类算法。它的基础思想是,对于给出的待分类项,求解在此项出现的条件下各个类别出现的概率,哪个最大,就认为此待分类项属 于哪个类别。1. 贝叶斯公式
朴素贝叶斯分类算法的核心是贝叶斯公式,即 P(B|A)=P(A|B)P(B)/P(A)。换个表达形式 会更清晰一些,P(类别|特征)=P(特征|类别)P(类别)/P(特征)。如果 X 是一个待分类的数据元组,由 n 个属性描述,H 是一个假设,如 X 属于类 C, 则分类问题中,计算概率P(H|X)的含义是,已知元组 X 的每个元素对应的属性值,求出;V 属于 C 类的概率。
例如,X 的属性值为 age=25, income=$5 000, H 对应的假设是,X 会买电脑。
- P(H|X):表示在已知某客户信息 age=25,income=$5 000 的条件下,该客户会买电脑的概率。
- P(H):表示对于任何给定的客户信息,该客户会购买电脑的概率。
- P(X|H):表示已知客户会买电脑,那么该客户的属性值为 age=25, income=$5 000 的概率。
- P(X):表示在所有的客户信息集合中,客户的属性值为 age=25, income=$5 000 的概率。
2. 工作原理
1)设 D 为样本训练集,每一个样本 X 都是由 n 个属性值组成的,即 X=(x1,x2,...,xn)),对应的属性集为 A1,A2,A3,…,An。2)假设有 m 个类标签,即C1,C2,…,Cm。对于某待分类元素 X,朴素分类器会把 P(C1|X) (i=1,2,…,m)值最大的类标签 C1 作为的类别。因此目标就是找出 P(C1|X) 中的最大值 (P(C1|X)=P(X|C1)P(C1)|P(X)
3)如果 n 的值特别大,也就是说样本元组有很多属性,那么对于 P(X|C1) 的计算会相当复杂。所以朴素贝叶斯算法做了一个假设,即对于样本元组中的每个属性,由于它们都互相条件独立,因此有 P(X|C1)=P(X1|C1)P(X2|C1)...(Xn|C1)。由于可以从训练集中计算出来,所以训练样本空间中,属于类 C1 并且对应属性 A1 的概率等于 x1 的数目除以样本空间中属于类 C1 的样本数目。
4)为了预测 X 所属的类标签,可以根据前面的步骤算出每一个类标签 C1 对应的 P(X|C1)P(C1) 值,当某一个类标签 C1,对于任意 j(1≤j≤m,j≠i),都有 P(X|C1)P(1)>P(X|C1)P(C1) 时,则认为 X 属于类标签 C1。
3. Spark MLlib 朴素贝叶斯算法
Spark MLlib 的朴素贝叶斯算法主要是计算每个类别的先验概率,各类别下各个特征属性的条件概率的,其分布式实现方法是对样本进行聚合操作,统计所有标签出现的次数、对应特征之和。聚合操作后,可以通过聚合结果计算先验概率、条件概率,得到朴素贝叶斯分类模型。预测时,根据模型的先验概率、条件概率,计算每个样本属于每个类别的概率,最后取最大项作为样本的类别。
Spark MLlib 支持 Multinomial Naive Bayes 和 Bernoulli Naive Bayes。Multinomial Naive Bayes 主要用于文本的主题分类,分析时会考虑单词出现的次数,即词频,而 Binarzied Multinomial Naive Bayes 不考虑词频,只考虑这个单词有没有出现,主要用于文本情绪分析。可以通过参数指定算法使用哪个模型。
Spark MLlib 的 Native Bayes 调用 train 方法进行分类训练,其参数如下所示。
def train(
input:RDD[LabeledPoint],
lambda:double,
modelType:String):NativeBayesModel
- input 表示输入数据集,每个 RDD 元素代表一个数据点,每个数据点包含标签和数据特征,对分类来讲,标签的值是 {0,1,...,numClasses-1}。
- lambda 是一个加法平滑参数,默认值是 1.0。
- modelType 用于指定是使用 Multinomial Native Bayes 还是 Bernoulli Native Bayes 算法模型,默认是 Multinomial Naive Bayes。
Spark MLlib 的 Native Bayes 的预测函数 NativeBayesModel.predict 方法与 DecisionTree 的预测函数一样,可以接收不同的数据输入参数,包向量、RDD,返回的是计算出来的预测值。
4. Spark MLlib 朴素贝叶斯算法实例
以表 1 的购买电脑样本数据作为训练数据集,使用 Multinomial Native Bayes 建立分类模型,然后使用构造好的分类模型,对一个数据样本进行分类预测。| age | income | student | credit_rating | buys_computer |
|---|---|---|---|---|
| ≤30 | high | no | fair | no |
| ≤30 | high | no | excellent | no |
| 31~40 | high | no | fair | yes |
| >40 | medium | no | fair | yes |
| >40 | low | yes | fair | yes |
| >40 | low | yes | excellent | no |
| 31~40 | low | yes | excellent | yes |
| ≤30 | medium | no | fair | no |
| ≤30 | low | yes | fair | yes |
| >40 | medium | yes | fair | yes |
| ≤30 | medium | yes | excellent | yes |
| 31~40 | medium | no | excellent | yes |
| 31~40 | high | yes | fair | yes |
| >40 | medium | no | excellent | no |
buys_computer,age income student credit_rating
其中,buys_computer 的取值为,no 为 0,yes 为 1;age 的取值为,≤30 为 0,31~40 为 1,>40 为 2;income 的取值为,low 为 0,medium 为 1,high 为 2;student 的取值为,no 为 0,yes 为 1,credit_rating 的取值为,fair 为 0,excellent 为 1。对应于表 1 的数据的前 3 行数据如下。
实现的代码如下所示:
import org.apache.spark.mllib.classification.{NaiveBayes,NaiveBayesModel}
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.regression.LabeledPoint
import org.apache.spark.{SparkContext,SparkConf}
object NaiveBayes {
def main (args : Array[String]) : Unit = {
val conf = new SparkConf().setMaster("local").setAppName("NaiveBayes")
val sc = new SparkContext(conf)
val path ="../data/sample_computer.data"
val data = sc.textFile(path)
val parsedData = data.map {
line =>
val parts = line.split(','))
LabeledPoint (parts(0).toDouble,Vectors.dense (parts(1).split('').map(_.toDouble)))
}
//样本划分 train 和 test 数据样本 60% 用于 train
val splits = parsedData.randomSplit(Array(0.6,0.4),seed = 11L)
val training = splits(0)
val test = splits(1)
//获得训练模型,第一个参数为数据,第二个参数为平滑参数,默认为1
val model = NaiveBayes.train(training,lambda = 1.0)
//对测试样本进行测试
val predictionAndLabel = test.map(p => (model.predict(p.features),p.label))
//对模型进行准确度分析
val accuracy = 1.0 *predictionAndLabel.filter (x => x._1 == x._2).count()/test.count.()
//打印一个预测值
printIn ("NaiveBayes精度------>" + accuracy)
printIn ("假如 age<=30, income=medium, student=yes,credit_rating=fair,是否购买电脑:" + model.predict(Vectors.dense(0.0,2.0,0.0,1.0)))
//保存model
val ModelPath = "../model/NativeBayes_model.obj"
model.save(sc.ModelPath)
}
}
5. 算法优缺点
朴素贝叶斯算法的主要优点就是算法逻辑简单,易于实现;同时,分类过程的时空开销小,只会涉及二维存储。理论上,朴素贝叶斯算法与其他分类方法相比,具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好,而在属性相关性较小时,朴素贝叶斯算法的性能最为良好。
所有教程
- C语言入门
- C语言编译器
- C语言项目案例
- 数据结构
- C++
- STL
- C++11
- socket
- GCC
- GDB
- Makefile
- OpenCV
- Qt教程
- Unity 3D
- UE4
- 游戏引擎
- Python
- Python并发编程
- TensorFlow
- Django
- NumPy
- Linux
- Shell
- Java教程
- 设计模式
- Java Swing
- Servlet
- JSP教程
- Struts2
- Maven
- Spring
- Spring MVC
- Spring Boot
- Spring Cloud
- Hibernate
- Mybatis
- MySQL教程
- MySQL函数
- NoSQL
- Redis
- MongoDB
- HBase
- Go语言
- C#
- MATLAB
- JavaScript
- Bootstrap
- HTML
- CSS教程
- PHP
- 汇编语言
- TCP/IP
- vi命令
- Android教程
- 区块链
- Docker
- 大数据
- 云计算