Apriori算法和FP-Tree算法简介
本节主要描述了基于 Apriori 算法的关联分析方法。为了克服 Apriori 算法在复杂度和效率方面的缺陷,本节还进一步的介绍了基于 FP-Tree 的频繁模式挖掘方法。
Apriori 性质:一个频繁项集的所有非空子集也必须是频繁项集。即假如项集 A 不满足最小支持度阈值,即 A 不是频繁的,则如果将项集 B 添加到项集 A 中,那么新项集(AUB)也不可能是频繁的。
Apriori 算法简单来说主要有以下几个步骤。
1)通过单遍扫描数据集,确定每个项的支持度。一旦完成这一步,就可得到所有频繁 1-项集的集合 F1。
2)使用上一次迭代发现的频繁(k-1)-项集,产生新的候选k-项集。
3)为了对候选项集的支持度计数,再次扫描一遍数据库,使用子集函数确定包含在每一个交易 t 中的所有候选 k-项集。
4)计算候选项集的支持度计数后,算法将删除支持度计数小于支持度阈值的所有候选项集。
5)重复步骤(2)、(3)、(4),当没有新的频繁项集产生时,算法结束。
Apriori 算法是个逐层算法,它使用“产生——测试”策略来发现频繁项集。在由(k-1)-项集产生 k-项集的过程中“新产生的 k-项集先要确定它的所有的(k-1)-项真子集都是频繁的,如果有一个不是频繁的,那么它可以从当前的候选项集中去掉。
产生候选项集的方法有以下几种。
2)
由 1-项集和(k-1)-项集生成 k-项集,然后再剪枝。这种方法是完全的,因为每一个频繁 k-项集都是由一个频繁(k-1)-项集和一个频繁 1-项集产生的。由于顺序的关系,这种方法会产生大量重复的频繁 k-项集。
3)
由两个频繁(k-1 )-项集生成候选 k-项集,但是两个频繁(k-1)-项集的前 k-2 项必须相同,最后一项必须相异。由于每个候选项集都是由一对频繁(k-1)-项集合并而成的,所以需要附加的候选剪枝步骤来确保该候选的其余 k-2 个子集是频繁的。
假设有频繁项集 Y,X 是 Y 的一个子集,那么如果规则 X→Y→X 不满足置信度阈值,则形如 X1→Y1→X1 的规则一定也不满足置信度阈值,其中,X1 是 X 的子集。根据该性质,假设由频繁项集 {a,b,c,d}产生关联规则,关联规则{b,c,d}→{a} 具有低置信度,则可以丢弃后件包含 a 的所有关联规则,如{c,d}→{a,b},{b,d}→{a,c} 等。
FP-Growth 算法是指,通过两次扫描事务数据集,把每个事务所包含的频繁项目按其支持度降序压缩存储到 FP-Tree 中。
在以后发现频繁模式的过程中,不需要再扫描事务数据集,而仅在 FP-Tree 中进行查找即可。通过递归调用 FP-Growth 的方法可直接产生频繁模式,因此在整个发现过程中也不需产生候选模式。由于只对数据集扫描两次,因此 FP-Growth 算法克服了 Apriori 算法中存在的问题,在执行效率上也明显好于 Apriori 算法。
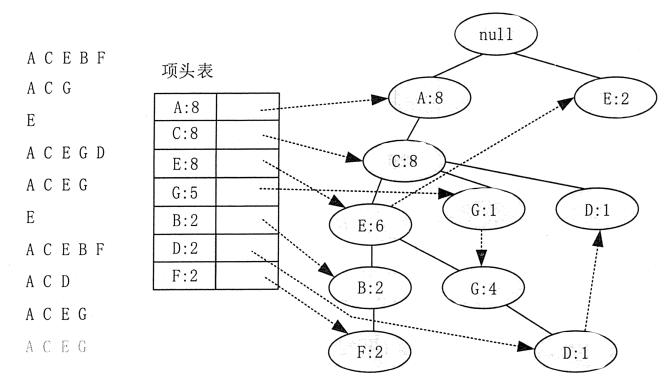
图 1 FP-Tree数据结构
第一部分是一个项头表,记录了所有的频繁 1-项集出现的次数,按照次数降序排列。例如, 在图 1 中,A 在所有 10 组数据中出现了 8 次,因此排在第一位。
第二部分是 FP-Tree,它将原始数据集映射到了內存中的一颗 FP-Tree。
第三部分是结点链表。所有项头表里的频繁 1—项集都是一个结点链表的头,它依次指向 FP-Tree 中该频繁 1-项集出现的位置。这样做主要是方便项头表和 FP-Tree 之间的联系查找和更新。
第二次扫描数据集,将读到的原始数据剔除非频繁 1-项集,并按照支持度降序排列。
在这个例子中有 10 条数据,首先第一次扫描数据并对 1-项集计数,发现 F、O、I、L、J、P、M、N 都只出现一次,支持度低于阈值(20%),因此它们不会出现在项头表中。将剩下的 A、C、E、G、B、D、F 按照支持度的大小降序排列,组成了项头表。
接着第二次,扫描数据,对每条数据剔除非频繁 1—项集,并按照支持度降序排列。例如,数据项 A、B, C、E、F、O 中的 O 是非频繁 1-项集,因此被剔除,只剩下了 A、B、C、E、F。 按照支持度的顺序排序,它变成了 A、C、E、B、F,其他的数据项以此类推。将原始数据集里的频繁 1-项集进行排序是为了在后面的 FP-Tree 的建立时,可以尽可能地共用祖先结点。
经过两次扫描,项头集已经建立,排序后的数据集也已经得到了,如图 2 所示。
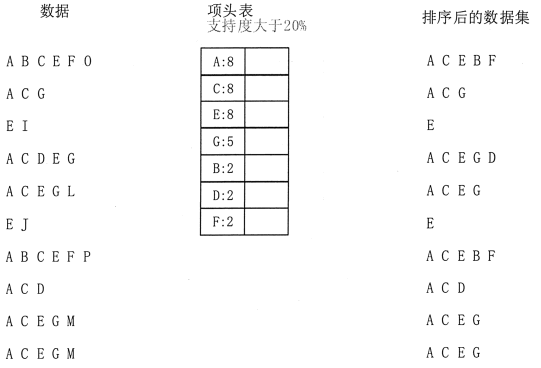
图 2 FP-Tree项头表示意
开始时 FP-Tree 没有数据,建立 FP-Tree 时要一条条地读入排序后的数据集,并将其插入 FP-Tree。插入时,排序靠前的结点是祖先结点,而靠后的是子孙结点。如果有共用的祖先,则对应的公用祖先结点计数加 1。插入后,如果有新结点出现,则项头表对应的结点会通过结点链表链接上新结点。直到所有的数据都插入到 FP-Tree 后,FP-Tree 的建立完成。
下面来举例描述 FP-Tree 的建立过程。首先,插入第一条数据 A、C、E、E、F,如图 3 所示。此时 FP-Tree 没有结点,因此 A、C、E、B、F 是一个独立的路径,所有结点的计数都为 1,项头表通过结点链表链接上对应的新增结点。
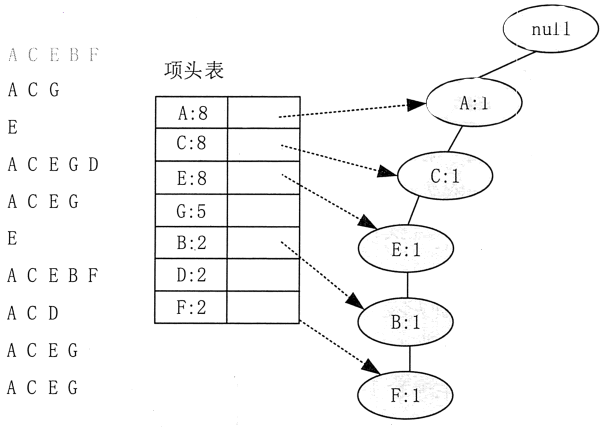
图 3 FP-Tree的构造示意1
接着插入数据 A、C、G,如图 4 所示。由于 A、C、G 和现有的 FP-Tree 可以有共有的祖先结点序列 A、C,因此只需要增加一个新结点 G,将新结点 G 的计数记为 1,同时 A 和 C 的计数加 1 成为 2。当然,对应的 G 结点的结点链表要更新。
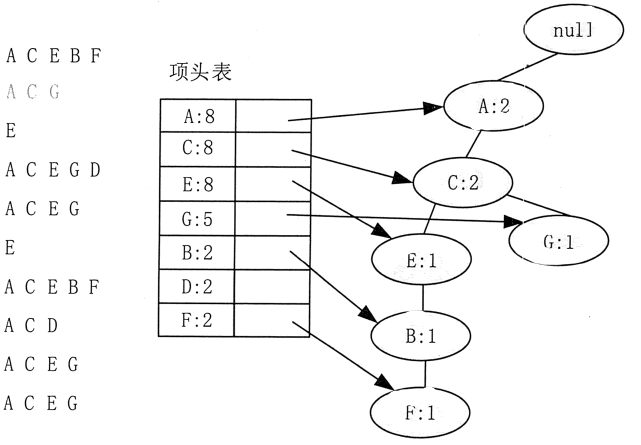
图 4 FP-Tree的构造示意2
用同样的办法可以更新后面 8 条数据,最后构成的 FP-Tree,如图 1 所示。由于原理类似,就不再逐步描述。
条件模式基是指以要挖掘的结点作为叶子结点所对应的 FP 子树。得到这个 FP 子树,将子树中每个结点的计数设置为叶子结点的计数,并删除计数低于支持度的结点。基于这个条件模式基,就可以递归挖掘得到频繁项集了。
还是以上面的例子来进行讲解。先从最底部的 F 结点开始,寻找 F 结点的条件模式基,由于 F 在 FP-Tree 中只有一个结点,因此候选就只有图 5 左边所示的一条路径,对应 {A:8,C:8,E:6,B:2,F:2}。接着将所有的祖先结点计数设置为叶子结点的计数,即 FP 子树变成 {A:2,C:2,E:2,B:2,F:2}。
条件模式基可以不写叶子结点,因此最终的 F 的条件模式基如图 5 右边所示。
基于条件模式基,很容易得到 F 的频繁 2-项集为 {A:2,F:2},{C:2,F:2},{E:2,F:2}, {B:2,F:2}。递归合并 2—项集,可得到频繁 3—项集为{A:2,C:2,F:2}, {A:2,E:2,F:2}, {A:2,B:2,F:2}, {C:2,E:2, F:2}, {C:2,B2, F:2}, {E:2,B2, F:2}。递归合并 3-项集,可得到频繁 4—项集为{A:2,C:2,E:2,F:2},{A:2,C:2,B2,F:2}, {C:2,E:2,B2,F:2}。一直递归下去,得到最大的频繁项集为频繁 5-项集,为 {A:2,C:2,E:2,B2,F:2}。
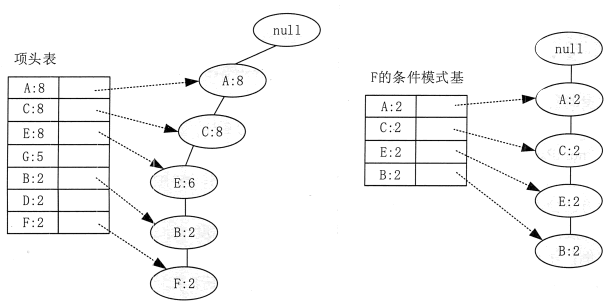
图 3 FP-Tree的挖掘示意1
F 结点挖掘完后,可以开始挖掘 D 结点。D 结点比 F 结点复杂一些,因为它有两个叶子结点,因此首先得到的 FP 子树如图 5左边所示。
接着将所有的祖先结点计数设置为叶子结点的计数,即变成 {A:2,C:2,E:1 G:1,D:1,D:1}。此时,E 结点和 G 结点由于在条件模式基里面的支持度低于阈值,所以被删除,最终,去除了低支持度结点和叶子结点后的 D 结点的条件模式基为 {A:2,C:2}。通过它,可以很容易得到 D 结点的频繁 2-项集为 {A:2,D:2},{C:2,D:2}。递归合并 2-项集,可得到频繁 3-项集为 {A:2,C:2,D:2}。D 结点对应的最大的频繁项集为频繁 3_项集。
用同样的方法可以递归挖掘到 B 的最大频繁项集为频繁 4-项集 {A:2,C:2,E:2,B2}。继续挖掘,可以递归挖掘到 G 的最大频繁项集为频繁 4-项集 {A:5,C:5,E:4,G:4},E 的最大频繁项集为频繁 3-项集 {A:6,C:6,E:6},C 的最大频繁项集为频繁 2-项集{A:8,C:8}。由于 A 的条件模式基为空,因此可以不用去挖掘了。
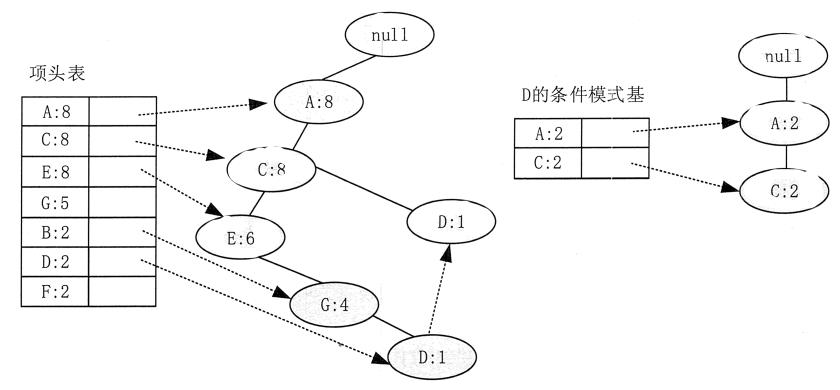
图 4 FP-Tree的挖掘示意2
至此得到了所有的频繁项集,如果只是要最大的频繁 k-项集,则从上面的分析可以看到,最大的频繁项集为 5-项集,包括{A:2,C:2,E:2,B:2,F:2}。
首先,通过调用 FPGrowth.run 方法构建 FP-Growth 树,树中将会存储频繁项集的数据信息,该方法会返回 FPGrowthModel;然后,调用 FPGrowthModel.generateAssociationRules 方法生成置信度高于阈值的关联规则,以及每个关联规则的置信度。
实例:导入训练数据集,使用 FP-Growth 算法挖掘出关联规则。该实例使用的数据存放在 fpg.data 文档中,提供了 6 个交易样本数据集。样本数据如下所示。
实现的代码如下所示。
部分频繁项集如下。
Apriori关联分析算法
Apriori 算法是挖掘产生关联规则所需频繁项集的基本算法,也是最著名的关联分析算法之一。1. Apriori 算法
Apriori 算法使用了逐层搜索的迭代方法,即用 k-项集探索(k+1)-项集。为提高按层次搜索并产生相应频繁项集的处理效率,Apriori 算法利用了一个重要性质,该性质还能有效缩小频繁项集的搜索空间。Apriori 性质:一个频繁项集的所有非空子集也必须是频繁项集。即假如项集 A 不满足最小支持度阈值,即 A 不是频繁的,则如果将项集 B 添加到项集 A 中,那么新项集(AUB)也不可能是频繁的。
Apriori 算法简单来说主要有以下几个步骤。
1)通过单遍扫描数据集,确定每个项的支持度。一旦完成这一步,就可得到所有频繁 1-项集的集合 F1。
2)使用上一次迭代发现的频繁(k-1)-项集,产生新的候选k-项集。
3)为了对候选项集的支持度计数,再次扫描一遍数据库,使用子集函数确定包含在每一个交易 t 中的所有候选 k-项集。
4)计算候选项集的支持度计数后,算法将删除支持度计数小于支持度阈值的所有候选项集。
5)重复步骤(2)、(3)、(4),当没有新的频繁项集产生时,算法结束。
Apriori 算法是个逐层算法,它使用“产生——测试”策略来发现频繁项集。在由(k-1)-项集产生 k-项集的过程中“新产生的 k-项集先要确定它的所有的(k-1)-项真子集都是频繁的,如果有一个不是频繁的,那么它可以从当前的候选项集中去掉。
产生候选项集的方法有以下几种。
1)蛮力法
从 2-项集开始以后所有的项集都是从 1-项集完全拼出来的。例如,3- 项集由 3 个 1-项集拼出,要列出所有的可能性。然后再按照剪枝算法剪枝,即确定当前的项集的所有(k-1)-项集是否都是频繁的。
2)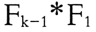 法
法
由 1-项集和(k-1)-项集生成 k-项集,然后再剪枝。这种方法是完全的,因为每一个频繁 k-项集都是由一个频繁(k-1)-项集和一个频繁 1-项集产生的。由于顺序的关系,这种方法会产生大量重复的频繁 k-项集。
3)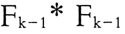 法
法
由两个频繁(k-1 )-项集生成候选 k-项集,但是两个频繁(k-1)-项集的前 k-2 项必须相同,最后一项必须相异。由于每个候选项集都是由一对频繁(k-1)-项集合并而成的,所以需要附加的候选剪枝步骤来确保该候选的其余 k-2 个子集是频繁的。
2. 由频繁项集产生关联规则
一旦从事务数据集中找出频繁项集,就可以直接由它们产生强关联规则,即满足最小支持度和最小置信度的规则。计算关联规则的置信度并不需要再次扫描事物数据集,因为这两个项集的支持度计数已经在频繁项集产生时得到。假设有频繁项集 Y,X 是 Y 的一个子集,那么如果规则 X→Y→X 不满足置信度阈值,则形如 X1→Y1→X1 的规则一定也不满足置信度阈值,其中,X1 是 X 的子集。根据该性质,假设由频繁项集 {a,b,c,d}产生关联规则,关联规则{b,c,d}→{a} 具有低置信度,则可以丢弃后件包含 a 的所有关联规则,如{c,d}→{a,b},{b,d}→{a,c} 等。
3. 算法优缺点
Apriori 算法作为经典的频繁项集产生算法,使用先验性质,大大提高了频繁项集逐层产生的效率,它简单易理解,数据集要求低。但是随着应用的深入,它的缺点也逐渐暴露出来,主要的性能瓶颈有以下两点。- 多次扫描事务数据集,需要很大的 I/O 负载。对每次 k 循环,对候选集 ck 中的每个元素都必须通过扫描数据集一次来验证其是否加入 lk。
- 可能产生庞大的候选集。候选项集的数量是呈指数级增长的,如此庞大的候选项集对时间和空间都是一种挑战。
FP-Tree关联分析算法
2000 年,Han Jiawei 等人提出了基于频繁模式树(Frequent Pattern Tree, FP—Tree)的发现频繁模式的算法 FP-Growth。其思想是构造一棵 FP-Tree,把数据集中的数据映射到树上,再根据这棵 FP-Tree 找出所有频繁项集。FP-Growth 算法是指,通过两次扫描事务数据集,把每个事务所包含的频繁项目按其支持度降序压缩存储到 FP-Tree 中。
在以后发现频繁模式的过程中,不需要再扫描事务数据集,而仅在 FP-Tree 中进行查找即可。通过递归调用 FP-Growth 的方法可直接产生频繁模式,因此在整个发现过程中也不需产生候选模式。由于只对数据集扫描两次,因此 FP-Growth 算法克服了 Apriori 算法中存在的问题,在执行效率上也明显好于 Apriori 算法。
1. FP—Tree 的构造
为了减少 I/O 次数,FP-Tree 算法引入了一些数据结构来临时存储数据。这个数据结构包括 3 部分:项头表、FP-Tree 和结点链接,如图 1 所示。
图 1 FP-Tree数据结构
第一部分是一个项头表,记录了所有的频繁 1-项集出现的次数,按照次数降序排列。例如, 在图 1 中,A 在所有 10 组数据中出现了 8 次,因此排在第一位。
第二部分是 FP-Tree,它将原始数据集映射到了內存中的一颗 FP-Tree。
第三部分是结点链表。所有项头表里的频繁 1—项集都是一个结点链表的头,它依次指向 FP-Tree 中该频繁 1-项集出现的位置。这样做主要是方便项头表和 FP-Tree 之间的联系查找和更新。
1)项头表的建立
建立 FP-Tree 需要首先建立项头表。第一次扫描数据集,得到所有频繁 1-项集的计数。然后删除支持度低于阈值的项,将频繁 1—项集放入项头表,并按照支持度降序排列。第二次扫描数据集,将读到的原始数据剔除非频繁 1-项集,并按照支持度降序排列。
在这个例子中有 10 条数据,首先第一次扫描数据并对 1-项集计数,发现 F、O、I、L、J、P、M、N 都只出现一次,支持度低于阈值(20%),因此它们不会出现在项头表中。将剩下的 A、C、E、G、B、D、F 按照支持度的大小降序排列,组成了项头表。
接着第二次,扫描数据,对每条数据剔除非频繁 1—项集,并按照支持度降序排列。例如,数据项 A、B, C、E、F、O 中的 O 是非频繁 1-项集,因此被剔除,只剩下了 A、B、C、E、F。 按照支持度的顺序排序,它变成了 A、C、E、B、F,其他的数据项以此类推。将原始数据集里的频繁 1-项集进行排序是为了在后面的 FP-Tree 的建立时,可以尽可能地共用祖先结点。
经过两次扫描,项头集已经建立,排序后的数据集也已经得到了,如图 2 所示。

图 2 FP-Tree项头表示意
2)FP-Tree 的建立
有了项头表和排序后的数据集,就可以开始 FP-Tree 的建立了。开始时 FP-Tree 没有数据,建立 FP-Tree 时要一条条地读入排序后的数据集,并将其插入 FP-Tree。插入时,排序靠前的结点是祖先结点,而靠后的是子孙结点。如果有共用的祖先,则对应的公用祖先结点计数加 1。插入后,如果有新结点出现,则项头表对应的结点会通过结点链表链接上新结点。直到所有的数据都插入到 FP-Tree 后,FP-Tree 的建立完成。
下面来举例描述 FP-Tree 的建立过程。首先,插入第一条数据 A、C、E、E、F,如图 3 所示。此时 FP-Tree 没有结点,因此 A、C、E、B、F 是一个独立的路径,所有结点的计数都为 1,项头表通过结点链表链接上对应的新增结点。

图 3 FP-Tree的构造示意1
接着插入数据 A、C、G,如图 4 所示。由于 A、C、G 和现有的 FP-Tree 可以有共有的祖先结点序列 A、C,因此只需要增加一个新结点 G,将新结点 G 的计数记为 1,同时 A 和 C 的计数加 1 成为 2。当然,对应的 G 结点的结点链表要更新。

图 4 FP-Tree的构造示意2
用同样的办法可以更新后面 8 条数据,最后构成的 FP-Tree,如图 1 所示。由于原理类似,就不再逐步描述。
2. FP-Tree 的挖掘
下面讲解如何从 FP-Tree 挖掘频繁项集。基于 FP-Tree、项头表及结点链表,首先要从项头表的底部项依次向上挖掘。对于项头表对应于 FP-Tree 的每一项,要找到它的条件模式基。条件模式基是指以要挖掘的结点作为叶子结点所对应的 FP 子树。得到这个 FP 子树,将子树中每个结点的计数设置为叶子结点的计数,并删除计数低于支持度的结点。基于这个条件模式基,就可以递归挖掘得到频繁项集了。
还是以上面的例子来进行讲解。先从最底部的 F 结点开始,寻找 F 结点的条件模式基,由于 F 在 FP-Tree 中只有一个结点,因此候选就只有图 5 左边所示的一条路径,对应 {A:8,C:8,E:6,B:2,F:2}。接着将所有的祖先结点计数设置为叶子结点的计数,即 FP 子树变成 {A:2,C:2,E:2,B:2,F:2}。
条件模式基可以不写叶子结点,因此最终的 F 的条件模式基如图 5 右边所示。
基于条件模式基,很容易得到 F 的频繁 2-项集为 {A:2,F:2},{C:2,F:2},{E:2,F:2}, {B:2,F:2}。递归合并 2—项集,可得到频繁 3—项集为{A:2,C:2,F:2}, {A:2,E:2,F:2}, {A:2,B:2,F:2}, {C:2,E:2, F:2}, {C:2,B2, F:2}, {E:2,B2, F:2}。递归合并 3-项集,可得到频繁 4—项集为{A:2,C:2,E:2,F:2},{A:2,C:2,B2,F:2}, {C:2,E:2,B2,F:2}。一直递归下去,得到最大的频繁项集为频繁 5-项集,为 {A:2,C:2,E:2,B2,F:2}。

图 3 FP-Tree的挖掘示意1
F 结点挖掘完后,可以开始挖掘 D 结点。D 结点比 F 结点复杂一些,因为它有两个叶子结点,因此首先得到的 FP 子树如图 5左边所示。
接着将所有的祖先结点计数设置为叶子结点的计数,即变成 {A:2,C:2,E:1 G:1,D:1,D:1}。此时,E 结点和 G 结点由于在条件模式基里面的支持度低于阈值,所以被删除,最终,去除了低支持度结点和叶子结点后的 D 结点的条件模式基为 {A:2,C:2}。通过它,可以很容易得到 D 结点的频繁 2-项集为 {A:2,D:2},{C:2,D:2}。递归合并 2-项集,可得到频繁 3-项集为 {A:2,C:2,D:2}。D 结点对应的最大的频繁项集为频繁 3_项集。
用同样的方法可以递归挖掘到 B 的最大频繁项集为频繁 4-项集 {A:2,C:2,E:2,B2}。继续挖掘,可以递归挖掘到 G 的最大频繁项集为频繁 4-项集 {A:5,C:5,E:4,G:4},E 的最大频繁项集为频繁 3-项集 {A:6,C:6,E:6},C 的最大频繁项集为频繁 2-项集{A:8,C:8}。由于 A 的条件模式基为空,因此可以不用去挖掘了。

图 4 FP-Tree的挖掘示意2
至此得到了所有的频繁项集,如果只是要最大的频繁 k-项集,则从上面的分析可以看到,最大的频繁项集为 5-项集,包括{A:2,C:2,E:2,B:2,F:2}。
3. MLlib 的 FP-Growth 算法实例
Spark MLlib 中 FP-Growth 算法的实现类 FPGrowth 具有以下参数。
class FPGrowth private (
private var minSupport: Double,
private var numPartitions: Int) extends Logging with Serializable
- minSupport 为频繁项集的支持度阈值,默认值为0.3。
- numPartitions 为数据的分区个数,也就是并发计算的个数。
首先,通过调用 FPGrowth.run 方法构建 FP-Growth 树,树中将会存储频繁项集的数据信息,该方法会返回 FPGrowthModel;然后,调用 FPGrowthModel.generateAssociationRules 方法生成置信度高于阈值的关联规则,以及每个关联规则的置信度。
实例:导入训练数据集,使用 FP-Growth 算法挖掘出关联规则。该实例使用的数据存放在 fpg.data 文档中,提供了 6 个交易样本数据集。样本数据如下所示。
r z h k p
z y x w v u t s
s x o n r
x z y m t s q e
z
x z y r q t p
实现的代码如下所示。
import org.apache.spark.mllib.fpm.FPGrowth import org.apache.spark.{SparkConf,SparkContext}
object FP_GrowthTest {
def main(args:Array[String]){
val conf = new SparkConf().setAppName("FPGrowthTest").setMaster("local[4]")
val sc = new SparkContext(conf)
//设置参数
val minSupport = 0.2 //最小支持度
val minConfidence = 0.8 //最小置信度
val numPartitions = 2 //数据分区数
//取出数据
val data = sc.textFile("data/mllib/fpg.data")
//把数据通过空格分割
val transactions = data.map (x=>x.split (""))
transactions.cache()
//创建一个 FPGrowth 的算法实列
val fpg = new FPGrowth()
fpg.setMinSupport(minSupport)
fpg.setNumPartitions(numPartitions)
//使用样本数据建立模型
val model = fpg.run(transactions)
//查看所有的频繁项集,并且列出它出现的次数
model.freqItemsets.collect().foreach(itemset=>{
printIn (itemset.items.mkString("[",",","]")+itemset.freq)
})
//通过置信度筛选出推荐规则
//antecedent 表示前项,consequent 表示后项
//confidence 表示规则的置信度
model.generateAssociationRules(minConfidence).collect().foreach(rule=>{printIn(rule.antecedent.mkString(",")+"-->" + rule.consequent.mkString("")+"-->"+ rule.confidence)
})
//查看规则生成的数量
printIn(model.generateAssociationRules (minConfidence).collect().length)
运行结果会打印频繁项集和关联规则。部分频繁项集如下。
[t] , 3
[t, x] ,3
[t, x, z] , 3
[t, z] , 3
[s] , 3
[s, t] , 2
[s, t, x] , 2
[s, t, x, z] , 2
[s, t, z], 2
[s, x] , 2
[s, x, z] , 2
s, t, x --> z --> 1.0
s, t, x --> y --> 1.0
q, x --> t --> 1.0
q, x --> y --> 1.0
q, x --> z --> 1.0
q, y, z --> t --> 1.0
q, y, z --> x --> 1.0
t, x, z --> y --> 1.0
q, x, z --> t --> 1.0
q, x, z --> y --> 1.0
所有教程
- C语言入门
- C语言编译器
- C语言项目案例
- 数据结构
- C++
- STL
- C++11
- socket
- GCC
- GDB
- Makefile
- OpenCV
- Qt教程
- Unity 3D
- UE4
- 游戏引擎
- Python
- Python并发编程
- TensorFlow
- Django
- NumPy
- Linux
- Shell
- Java教程
- 设计模式
- Java Swing
- Servlet
- JSP教程
- Struts2
- Maven
- Spring
- Spring MVC
- Spring Boot
- Spring Cloud
- Hibernate
- Mybatis
- MySQL教程
- MySQL函数
- NoSQL
- Redis
- MongoDB
- HBase
- Go语言
- C#
- MATLAB
- JavaScript
- Bootstrap
- HTML
- CSS教程
- PHP
- 汇编语言
- TCP/IP
- vi命令
- Android教程
- 区块链
- Docker
- 大数据
- 云计算